Joidenkin hahmojen painopisteiden sijainnit. Tasaisten kuvioiden painopisteen koordinaattien määrittäminen Epäsäännöllisen muotoisen litteän kappaleen painopisteen löytäminen

Edellä saatujen yleisten kaavojen perusteella on mahdollista osoittaa erityisiä menetelmiä kappaleiden painopisteiden koordinaattien määrittämiseksi.

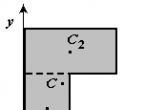
1. Symmetria. Jos homogeenisella kappaleella on taso, akseli tai symmetriakeskus (kuva 7), niin sen painopiste sijaitsee vastaavasti symmetriatasolla, symmetria-akselilla tai symmetriakeskipisteellä.

Kuva 7

2. Halkaisu. Runko on jaettu äärelliseen määrään osia (kuva 8), joista jokaiselle tunnetaan painopisteen sijainti ja pinta-ala.

Kuva 8

3.Negatiivisten alueiden menetelmä. Erityinen osiointimenetelmän tapaus (kuva 9). Se koskee kappaleita, joissa on aukko, jos kappaleen painopisteet ilman leikkausta ja leikkausta tunnetaan. Leikatun levyn muodossa olevaa kappaletta edustaa kiinteän levyn (ilman leikkausta) yhdistelmä, jonka pinta-ala on S 1 ja leikatun osan pinta-ala S 2 .

Kuva 9

4.ryhmittelymenetelmä. Se on hyvä lisä kahteen viimeiseen menetelmään. Kun kuvio on hajotettu sen osiin elementteihin, on kätevää yhdistää osa niistä uudelleen, jotta ratkaisua voidaan yksinkertaistaa ottamalla huomioon tämän ryhmän symmetria.

Joidenkin homogeenisten kappaleiden painopisteet.

1) Ympyränkaaren painopiste. Harkitse kaaria AB säde R keskikulmalla. Symmetrian vuoksi tämän kaaren painopiste sijaitsee akselilla Härkä(Kuva 10).

Kuva 10

Etsitään koordinaatit kaavan avulla. Voit tehdä tämän valitsemalla kaaresta AB elementti MM' pituus , jonka sijainti määräytyy kulman mukaan . Koordinoi X elementti MM' tulee . Korvaa nämä arvot X ja d l ja kun otetaan huomioon, että integraalia on jatkettava koko kaaren pituudelle, saadaan:

missä L- kaaren pituus AB, yhtä kuin .

Sieltä lopulta huomaamme, että ympyränkaaren painopiste sijaitsee sen symmetria-akselilla etäisyyden päässä keskustasta NOIN yhtä kuin

jossa kulma mitataan radiaaneina.

2) Kolmion alueen painopiste. Harkitse tasossa olevaa kolmiota Oxy, jonka kärkikoordinaatit tunnetaan: A i(x i,y i), (i= 1,2,3). Kolmion murtaminen kapeiksi nauhoiksi sivun suuntaisesti MUTTA 1 MUTTA 2 , tulemme siihen tulokseen, että kolmion painopisteen tulee kuulua mediaaniin MUTTA 3 M 3 (kuvio 11).

Kuva 11

Kolmion murtaminen sivun suuntaisiksi nauhoiksi MUTTA 2 MUTTA 3 , voit varmistaa, että sen on oltava mediaanilla MUTTA 1 M yksi . Tällä tavoin, kolmion painopiste on sen mediaanien leikkauspisteessä, joka, kuten tiedät, erottaa kolmannen osan kustakin mediaanista vastaavalta puolelta laskettuna.

Etenkin mediaanille MUTTA 1 M 1 saamme, koska pisteen koordinaatit M 1 on kärjen koordinaattien aritmeettinen keskiarvo MUTTA 2 ja MUTTA 3:

x c = x 1 + (2/3)∙(x M 1 - x 1) = x 1 + (2/3)∙[(x 2 + x 3)/2-x 1 ] = (x 1 +x 2 +x 3)/3.

Siten kolmion painopisteen koordinaatit ovat sen kärkien koordinaattien aritmeettinen keskiarvo:

x c =(1/3)Σ x i ; y c =(1/3)Σ y i.

3) Pyöreän sektorin alueen painopiste. Tarkastellaan säteisen ympyrän sektoria R jonka keskikulma on 2α ja joka sijaitsee symmetrisesti akselin ympäri Härkä(Kuvio 12) .

Se on selvää y c = 0, ja etäisyys ympyrän keskipisteestä, josta tämä sektori leikataan, sen painopisteeseen voidaan määrittää kaavalla:

Kuva 12

Helpoin tapa laskea tämä integraali on jakaa integrointialue alkeissektoreiksi kulmalla dφ. Ensimmäisen kertaluvun äärettömiin pieniin määriin asti tällainen sektori voidaan korvata kolmiolla, jonka kanta on yhtä suuri kuin R× dφ ja korkeus R. Tällaisen kolmion pinta-ala dF=(1/2)R 2 ∙dφ, ja sen painopiste on 2/3:n etäisyydellä R ylhäältä, joten laitamme kohtaan (5). x = (2/3)R∙cosφ. Korvataan kohtaan (5) F= α R 2, saamme:

Viimeisen kaavan avulla laskemme erityisesti etäisyyden painopisteeseen puoliympyrä.

Korvaamalla kohdan (2) α = π/2, saamme: x c = (4R)/(3π) ≅ 0,4 R .

Esimerkki 1 Määritetään kuvan 1 mukaisen homogeenisen kappaleen painopiste. 13.

Kuva 13

Runko on homogeeninen ja koostuu kahdesta symmetrisestä osasta. Niiden painopisteiden koordinaatit:

Niiden määrät:

Siksi kehon painopisteen koordinaatit

Esimerkki 2 Etsi suorassa kulmassa taivutetun levyn painopiste. Mitat - piirustuksessa (kuva 14).

Kuva 14

Painopisteiden koordinaatit:

Neliöt:

Riisi. 6.5

Esimerkki 3 Neliömäisestä arkista cm leikataan neliömäinen reikä cm (kuva 15). Etsi arkin painopiste.

Kuva 15

Tässä ongelmassa on kätevämpää jakaa runko kahteen osaan: suureen neliöön ja neliömäiseen reikään. Vain reiän pinta-alaa tulisi pitää negatiivisena. Sitten levyn ja reiän painopisteen koordinaatit:

koordinoida koska keholla on symmetria-akseli (diagonaali).

Esimerkki 4 Vaijerikannatin (kuva 16) koostuu kolmesta samanpituisesta osasta l.

Kuva 16

Osuuksien painopisteiden koordinaatit:

Siksi koko kiinnikkeen painopisteen koordinaatit:

Esimerkki 5 Määritä ristikon painopisteen sijainti, jonka kaikilla tangoilla on sama lineaarinen tiheys (kuva 17).

Muista, että fysiikassa kappaleen tiheys ρ ja sen ominaispaino g liittyvät toisiinsa suhteella: γ= ρ g, missä g- painovoiman kiihtyvyys. Tällaisen homogeenisen kappaleen massan löytämiseksi sinun on kerrottava tiheys sen tilavuudella.

Kuva 17

Termi "lineaarinen" tai "lineaarinen" tiheys tarkoittaa, että ristikon tangon massan määrittämiseksi lineaarinen tiheys on kerrottava tämän tangon pituudella.

Voit ratkaista ongelman käyttämällä osiointimenetelmää. Esittämällä annettua ristikkoa 6 yksittäisen tangon summana, saamme:

missä L i pituus i- tilan sauva ja x i, y i ovat sen painopisteen koordinaatit.

Tämän ongelman ratkaisua voidaan yksinkertaistaa ryhmittelemällä viimeiset 5 ristikkotankoa. On helppo nähdä, että ne muodostavat hahmon, jonka symmetriakeskus sijaitsee neljännen tangon keskellä, missä tämän sauvaryhmän painopiste sijaitsee.

Näin ollen tietty ristikko voidaan edustaa vain kahden sauvaryhmän yhdistelmällä.

Ensimmäinen ryhmä koostuu sen ensimmäisestä sauvasta L 1 = 4 m, x 1 = 0 m, y 1 = 2 m. Toinen sauvaryhmä koostuu viidestä tangosta, joille L 2 = 20 m, x 2 = 3 m, y 2 = 2 m.

Tilan painopisteen koordinaatit löytyvät kaavasta:

x c = (L 1 ∙x 1 +L 2 ∙x 2)/(L 1 + L 2) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙y 1 +L 2 ∙y 2)/(L 1 + L 2) = (4∙2 + 20∙2)/24 = 2 m.

Huomaa, että keskellä FROM sijaitsee yhdistävällä linjalla FROM 1 ja FROM 2 ja jakaa segmentin FROM 1 FROM 2 liittyen: FROM 1 FROM/SS 2 = (x c - x 1)/(x 2 - x c ) = L 2 /L 1 = 2,5/0,5.

Kysymyksiä itsetutkiskelua varten

Mikä on rinnakkaisten voimien keskipiste?

Miten rinnakkaisten voimien keskipisteen koordinaatit määritetään?

Kuinka määrittää yhdensuuntaisten voimien keskus, joiden resultantti on nolla?

Mikä on rinnakkaisten voimien keskuksen ominaisuus?

Millä kaavoilla lasketaan rinnakkaisten voimien keskipisteen koordinaatit?

Mikä on kehon painopiste?

Miksi Maan vetovoimat, jotka vaikuttavat kehon pisteeseen, voidaan pitää rinnakkaisten voimien järjestelmänä?

Kirjoita muistiin kaava epähomogeenisten ja homogeenisten kappaleiden painopisteen sijainnin määrittämiseksi, kaava litteiden osien painopisteen sijainnin määrittämiseksi?

Kirjoita muistiin kaava yksinkertaisten geometristen muotojen painopisteen sijainnin määrittämiseksi: suorakulmio, kolmio, puolisuunnikkaan ja puoliympyrän?

Mitä kutsutaan alueen staattiseksi momentiksi?

Anna esimerkki kappaleesta, jonka painopiste sijaitsee kehon ulkopuolella.

Miten symmetriaominaisuuksia käytetään kappaleiden painopisteiden määrittämiseen?

Mikä on negatiivisten painojen menetelmän ydin?

Missä ympyränkaaren painopiste sijaitsee?

Millä graafisella konstruktiolla voidaan löytää kolmion painopiste?

Kirjoita muistiin kaava, joka määrittää ympyränmuotoisen sektorin painopisteen.

Johda samanlainen kaava ympyränmuotoiselle segmentille käyttämällä kaavoja, jotka määrittävät kolmion ja ympyränmuotoisen sektorin painopisteet.

Millä kaavoilla lasketaan homogeenisten kappaleiden, tasokuvioiden ja suorien painopisteiden koordinaatit?

Mitä kutsutaan litteän hahmon alueen staattiseksi momentiksi suhteessa akseliin, miten se lasketaan ja mikä mitta sillä on?

Kuinka määrittää alueen painopisteen sijainti, jos sen yksittäisten osien painopisteiden sijainti tunnetaan?

Mitä apulauseita käytetään painopisteen sijainnin määrittämiseen?

Aihe on suhteellisen helppo hallita, mutta se on erittäin tärkeä materiaalien lujuuskulkua tutkittaessa. Päähuomio tässä tulee kiinnittää ongelmien ratkaisemiseen sekä litteillä että geometrisilla muodoilla sekä tavallisilla valssatuilla profiileilla.

Kysymyksiä itsehillintää varten

1. Mikä on yhdensuuntaisten voimien keskipiste?

Yhdensuuntaisten voimien keskipiste on piste, jonka kautta tietyissä pisteissä käytettyjen rinnakkaisten voimien resultanttijärjestelmän viiva kulkee näiden voimien suunnan muutoksilla avaruudessa.

2. Kuinka löytää yhdensuuntaisten voimien keskipisteen koordinaatit?

Yhdensuuntaisten voimien keskipisteen koordinaattien määrittämiseksi käytämme Varignon-lausetta.

Akselin suhteellinen x

Mx(R) = ΣMx(Fk), - y CR = Σy kFk Ja y C = Σy kFk /Σ Fk .

Akselin suhteellinen y

M y (R) = ΣM y (Fk), - x C R = Σx kFk Ja x C = Σx kFk /Σ Fk .

Koordinaattien määrittämiseksi z C , käännä kaikkia voimia 90° niin, että ne tulevat yhdensuuntaisiksi akselin kanssa y (Kuva 1.5, b). Sitten

M z (R) = ΣM z (Fk), - z CR = Σz kFk Ja z C = Σz kFk /Σ Fk .

Siksi kaava yhdensuuntaisten voimien keskipisteen sädevektorin määrittämiseksi saa muodon

r C = Σr kFk /Σ Fk.

3. Mikä on kehon painopiste?

Painovoiman keskipiste - piste, joka on poikkeuksetta yhteydessä kiinteään kappaleeseen, jonka läpi tämän kappaleen hiukkasiin vaikuttavien painovoimavoimien resultantti kulkee missä tahansa kappaleen kohdassa avaruudessa. Homogeeniselle kappaleelle, jossa on symmetriakeskus (ympyrä, pallo, kuutio jne.), painopiste sijaitsee kappaleen symmetriakeskuksessa. Jäykän kappaleen painopisteen sijainti on sama kuin sen massakeskuksen sijainti.

4. Kuinka löytää suorakulmion, kolmion, ympyrän painopiste?

Kolmion painopisteen löytämiseksi sinun on piirrettävä kolmio - kuva, joka koostuu kolmesta segmentistä, jotka on yhdistetty toisiinsa kolmessa pisteessä. Ennen kuin löydät hahmon painopisteen, sinun on mitattava viivaimella kolmion yhden sivun pituus. Aseta sivun keskelle merkki, jonka jälkeen yhdistä vastakkainen kärkipiste ja segmentin keskikohta linjalla, jota kutsutaan mediaaniksi. Toista sama algoritmi kolmion toiselle puolelle ja sitten kolmannelle. Työsi tuloksena on kolme mediaania, jotka leikkaavat yhdessä pisteessä, joka on kolmion painopiste. Jos on tarpeen määrittää homogeenisen rakenteen pyöreän kiekon painopiste, etsi ensin ympyrän halkaisijoiden leikkauspiste. Se tulee olemaan tämän kehon painopiste. Kun otetaan huomioon sellaiset hahmot kuin pallo, vanne ja homogeeninen suorakaiteen muotoinen suuntaissärmiö, voimme varmuudella sanoa, että vanteen painopiste on hahmon keskellä, mutta sen pisteiden ulkopuolella pallon painopiste on pallon geometrinen keskipiste ja jälkimmäisessä tapauksessa painopiste on suorakaiteen muotoisen suuntaissärmiön leikkauslävistäjät.

5. Kuinka löytää tasaisen komposiittileikkauksen painopisteen koordinaatit?

Ositusmenetelmä: jos litteä kuva voidaan jakaa äärelliseen määrään sellaisia osia, joista jokaiselle tunnetaan painopisteen sijainti, niin koko kuvion painopisteen koordinaatit määritetään kaavoilla:

XC = (skxk)/S; Y C = ( s k y k) / S,

missä x k, y k ovat kuvion osien painopisteiden koordinaatit;

s k - niiden alue;

S \u003d s k - koko kuvion pinta-ala.

6. Painopiste

1. Missä tapauksessa painopisteen määrittämiseksi riittää laskemalla yksi koordinaatti?

Ensimmäisessä tapauksessa painopisteen määrittämiseksi riittää yhden koordinaatin määrittäminen.Keho on jaettu äärelliseen määrään osia, joista jokaisella on painopisteen sijainti C ja alue S tiedossa. Esimerkiksi kehon projektio tasoon xOy (Kuva 1.) voidaan esittää kahtena litteänä kuviona, joissa on pinta-alat S1 Ja S2 (S = S 1 + S 2 ). Näiden lukujen painopisteet ovat pisteissä C 1 (x 1, y 1) Ja C 2 (x 2 , y 2) . Silloin kehon painopisteen koordinaatit ovat

Koska kuvien keskipisteet ovat y-akselilla (x = 0), löydämme vain koordinaatin Meille.

2 Miten kuvan 4 reiän pinta-ala otetaan huomioon kuvion painopisteen määrityskaavassa?

Negatiivinen massa -menetelmä

Tämä menetelmä koostuu siitä, että kehoa, jossa on vapaita onteloita, pidetään kiinteänä ja vapaiden onteloiden massaa pidetään negatiivisena. Kaavojen muoto kehon painopisteen koordinaattien määrittämiseksi ei muutu.

Siten määritettäessä kappaleen painopistettä, jossa on vapaita onteloita, tulisi käyttää osiointimenetelmää, mutta onteloiden massaa tulisi pitää negatiivisena.

on idea yhdensuuntaisten voimien keskipisteestä ja sen ominaisuuksista;

tietää kaavat litteiden kuvioiden painopisteen koordinaattien määrittämiseksi;

pystyä määrittää yksinkertaisten geometristen kuvioiden ja standardivalssattujen profiilien tasaisten kuvioiden painopisteen koordinaatit.

KINEMATIIKAN JA DYNAMIIKAN ELEMENTIT
Kun olet tutkinut pisteen kinematiikkaa, kiinnitä huomiota siihen, että pisteen suoraviivaiselle liikkeelle, sekä epätasaiselle että tasaiselle, on aina ominaista normaali (keskipetaalinen) kiihtyvyys. Kappaleen translaatioliikkeessä (jolle on ominaista minkä tahansa sen pisteen liike) voidaan soveltaa kaikkia pisteen kinematiikan kaavoja. Kaavoilla, joilla määritetään kiinteän akselin ympäri pyörivän kappaleen kulma-arvot, on täydellinen semanttinen analogia translaationaalisesti liikkuvan kappaleen vastaavien lineaaristen arvojen määrittämiskaavojen kanssa.

Aihe 1.7. Pistekinematiikka
Aihetta tutkiessasi kiinnitä huomiota kinematiikan peruskäsitteisiin: kiihtyvyys, nopeus, polku, etäisyys.

Kysymyksiä itsehillintää varten

1. Mikä on levon ja liikkeen käsitteiden suhteellisuus?

Mekaaninen liike on muutos kehon tai (sen osien) liikkeessä avaruudessa suhteessa muihin kappaleisiin ajan kuluessa. Heitetyn kiven lento, pyörän pyöriminen ovat esimerkkejä mekaanisesta liikkeestä.

2. Määrittele kinematiikan peruskäsitteet: lentorata, etäisyys, polku, nopeus, kiihtyvyys, aika.

Nopeus on pisteen liikkeen kinemaattinen mitta, joka kuvaa sen sijainnin muutosnopeutta avaruudessa. Nopeus on vektorisuure, eli sille ei ole ominaista vain moduuli (skalaarikomponentti), vaan myös suunta avaruudessa.

Kuten fysiikasta tiedetään, tasaisella liikkeellä nopeus voidaan määrittää aikayksikköä kohti kuljetun polun pituudella: v = s / t = const (oletetaan, että polun ja ajan origo ovat samat). Suoraviivaisessa liikkeessä nopeus on vakio sekä absoluuttisessa arvossa että suunnassa, ja sen vektori osuu yhteen lentoradan kanssa.

Nopeuden yksikkö järjestelmässä SI määritetään suhteella pituus/aika, eli m/s.

Kiihtyvyys on ajankohdan nopeuden muutoksen kinemaattinen mitta. Toisin sanoen kiihtyvyys on nopeuden muutosnopeus.
Kuten nopeus, myös kiihtyvyys on vektorisuure, eli sille ei ole ominaista vain moduuli, vaan myös suunta avaruudessa.

Suoraviivaisessa liikkeessä nopeusvektori osuu aina yhteen lentoradan kanssa ja siksi myös nopeudenmuutosvektori osuu yhteen lentoradan kanssa.

Fysiikan kurssista tiedetään, että kiihtyvyys on nopeuden muutosta aikayksikköä kohden. Jos lyhyen ajan Δt pisteen nopeus muuttui Δv, niin tämän ajanjakson keskikiihtyvyys oli: a cp = Δv/Δt.

Keskikiihtyvyys ei anna käsitystä nopeuden muutoksen todellisesta suuruudesta kullakin ajanhetkellä. Samalla on selvää, että mitä lyhyempi tarkastelujakso, jonka aikana nopeuden muutos tapahtui, sitä lähempänä todellista (hetkellistä) kiihtyvyyden arvo on.
Tästä johtuu määritelmä: todellinen (hetkellinen) kiihtyvyys on raja, johon keskikiihtyvyys pyrkii, kun Δt pyrkii nollaan:

a = lim a cf kohdassa t→0 tai lim Δv/Δt = dv/dt.

Ottaen huomioon, että v \u003d ds / dt, saamme: a \u003d dv / dt \u003d d 2 s / dt 2.

Todellinen kiihtyvyys suoraviivaisessa liikkeessä on yhtä suuri kuin nopeuden ensimmäinen derivaatta tai koordinaatin toinen derivaatta (etäisyys liikkeen alkupisteestä) ajan suhteen. Kiihtyvyyden yksikkö on metri jaettuna toisella neliöllä (m/s 2).

Liikerata- viiva avaruudessa, jota pitkin materiaalipiste liikkuu.
Tapa on polun pituus. Kuljettu matka l on yhtä suuri kuin kappaleen jossakin ajassa t kulkeman liikeradan kaaren pituus. Polku on skalaariarvo.

Etäisyys määrittää pisteen sijainnin sen liikeradalla ja mitataan jostakin origosta. Etäisyys on algebrallinen suure, koska riippuen pisteen sijainnista origon suhteen ja etäisyyden akselin hyväksytystä suunnasta, se voi olla sekä positiivinen että negatiivinen. Toisin kuin etäisyys, pisteen kulkema polku määräytyy aina positiivisella luvulla. Polku osuu yhteen etäisyyden itseisarvon kanssa vain, jos pisteen liike alkaa origosta ja seuraa polkua yhteen suuntaan.

Yleisessä pisteen liikkeen tapauksessa polku on yhtä suuri kuin pisteen tietyn ajanjakson aikana kulkemien etäisyyksien absoluuttisten arvojen summa:

3. Millä tavoin pisteen liikelaki voidaan antaa?

1. Luonnollinen tapa asettaa pisteen liike.

Luonnollisella liikkeen määrittelymenetelmällä oletetaan määrittävän pisteen liikkeen parametrit liikkuvassa vertailujärjestelmässä, jonka alku on sama kuin liikkuva piste ja akselit ovat tangentti, normaali ja binormaali. pisteen liikerata kussakin sen sijainnissa. Pisteen liikelain asettamiseksi luonnollisella tavalla on välttämätöntä:

1) tuntea liikeradan;

2) aseta vertailupiste tälle käyrälle;

3) muodostaa positiivinen liikesuunta;

4) anna pisteen liikelaki tätä käyrää pitkin, ts. ilmaisee etäisyyden origosta käyrän pisteen sijaintiin tiettynä ajankohtana ∪OM=S(t) .

2.Vektorimenetelmä pisteen liikkeen määrittämiseen

Tässä tapauksessa pisteen sijainti tasossa tai avaruudessa määräytyy vektorifunktiolla. Tämä vektori piirretään origoksi valitusta kiinteästä pisteestä, jonka pää määrittää liikkuvan pisteen sijainnin.

3. Koordinaattimenetelmä pisteen liikkeen määrittämiseksi

Valitussa koordinaattijärjestelmässä liikkuvan pisteen koordinaatit annetaan ajan funktiona. Suorakaiteen muotoisessa suorakulmaisessa koordinaattijärjestelmässä nämä ovat yhtälöt:

4. Miten pisteen todellisen nopeuden vektori suuntautuu kaarevan liikkeen aikana?

Kun piste liikkuu epätasaisesti, sen nopeuden moduuli muuttuu ajan myötä.
Kuvittele piste, jonka liike on annettu luonnollisella tavalla yhtälöllä s = f(t).

Jos piste on kulkenut lyhyen ajan Δt polkua Δs, sen keskinopeus on yhtä suuri:

vav = ∆s/∆t.

Keskinopeus ei anna käsitystä todellisesta nopeudesta tietyllä hetkellä (todellista nopeutta kutsutaan muuten hetkelliseksi). Ilmeisesti mitä lyhyemmälle aikavälille keskinopeus määritetään, sitä lähempänä sen arvo on hetkellistä nopeutta.

Todellinen (hetkellinen) nopeus on raja, johon keskinopeus pyrkii, kun Δt pyrkii nollaan:

v = lim v cf kohdassa t → 0 tai v = lim (Δs/Δt) = ds/dt.

Siten todellisen nopeuden numeerinen arvo on v = ds/dt.
Todellinen (hetkellinen) nopeus minkä tahansa pisteen liikkeelle on yhtä suuri kuin koordinaatin ensimmäinen derivaatta (eli etäisyys liikkeen alkupisteestä) ajan suhteen.

Kun Δt pyrkii nollaan, myös Δs pyrkii nollaan, ja kuten olemme jo havainneet, nopeusvektori suunnataan tangentiaalisesti (eli se osuu yhteen todellisen nopeusvektorin v kanssa). Tästä seuraa, että ehdollisen nopeusvektorin v p raja, joka on yhtä suuri kuin pisteen siirtymävektorin ja äärettömän pienen aikavälin suhteen raja, on yhtä suuri kuin pisteen todellinen nopeusvektori.

5. Miten pisteen tangentti- ja normaalikiihtyvyydet suunnataan?

Kiihtyvyysvektorin suunta on sama kuin nopeuden muutoksen suunta Δ = - 0

Tangentiaalinen kiihtyvyys tietyssä pisteessä on suunnattu tangentiaalisesti pisteen lentoradalle; jos liikettä kiihdytetään, tangentiaalikiihtyvyysvektorin suunta osuu yhteen nopeusvektorin suunnan kanssa; jos liike on hidasta, tangentiaalikiihtyvyysvektorin suunta on vastakkainen nopeusvektorin suuntaan.

6. Mitä liikettä piste tekee, jos tangentiaalinen kiihtyvyys on nolla ja normaali ei muutu ajan myötä?

Tasainen kaareva liike jolle on tunnusomaista, että nopeuden numeerinen arvo on vakio ( v= vakio), nopeus muuttuu vain suuntaan. Tässä tapauksessa tangentiaalinen kiihtyvyys on nolla, koska v= vakio(Kuva b),

ja normaali kiihtyvyys ei ole nolla, koska r - lopullinen arvo.

7. Miltä kinemaattiset kuvaajat näyttävät tasaisella ja yhtä vaihtelevalla liikkeellä?

Tasaisella liikkeellä keho kattaa yhtä suuret etäisyydet kaikilla yhtäläisin aikavälein. Tasaisen suoraviivaisen liikkeen kinemaattista kuvausta varten koordinaattiakseli HÄRKÄ kätevä sijoittaa liikeradalle. Kehon asento tasaisen liikkeen aikana määritetään asettamalla yksi koordinaatti x. Siirtymävektori ja nopeusvektori suunnataan aina koordinaattiakselin suuntaisesti HÄRKÄ. Siksi siirtymä ja nopeus suoraviivaisen liikkeen aikana voidaan projisoida akselille HÄRKÄ ja pitää niiden projektioita algebrallisina suureina.

Tasaisella liikkeellä reitti muuttuu lineaarisen suhteen mukaan. koordinaateissa. Kaavio on kalteva viiva.

Aiheen opiskelun tuloksena opiskelijan tulee:

on idea tilasta, ajasta, liikeradalta; keskimääräinen ja todellinen nopeus;

tietää tapoja määrittää pisteen liike; pisteen liikkeen parametrit tiettyä lentorataa pitkin.

Luento 4. Painopiste.

Tämä luento kattaa seuraavat kysymykset

1. Jäykän kappaleen painopiste.

2. Epähomogeenisten kappaleiden painopisteiden koordinaatit.

3. Homogeenisten kappaleiden painopisteiden koordinaatit.

4. Painopisteiden koordinaattien määritysmenetelmät.

5. Joidenkin homogeenisten kappaleiden painopisteet.

Näiden asioiden tutkiminen on jatkossa tarpeen kappaleiden liikkeen dynamiikan tutkimiseksi ottaen huomioon liukukitka ja vierintäkitka, mekaanisen järjestelmän massakeskuksen liikkeen dynamiikka, kineettiset momentit, ongelmien ratkaisemiseksi. tieteenalalla "Materiaalien lujuus".

Tuo rinnakkaiset voimat.

Kun on tarkasteltu pelkistystä tasaisen järjestelmän ja mielivaltaisen spatiaalisen voimien järjestelmän keskipisteeseen, palataan taas yhdensuuntaisten voimien järjestelmän yksittäistapauksen tarkasteluun.

Tuo kaksi rinnakkaista voimaa.

Harkittaessa tällaista voimajärjestelmää, seuraavat kolme vähennystapausta ovat mahdollisia.

1. Kahden kollineaarisen voiman järjestelmä. Tarkastellaan kahden samansuuntaisen ja samaan suuntaan suunnatun voiman järjestelmää P Ja K, sovelletaan kohdissa MUTTA Ja SISÄÄN. Oletetaan, että voimat ovat kohtisuorassa tähän segmenttiin nähden (kuva 1, mutta).

FROM, joka kuuluu segmenttiin AB ja täyttää ehdon:

AC/SW = K/P.(1)

Pääjärjestelmän vektori RC = P + K modulo on yhtä suuri kuin näiden voimien summa: RC = P + K.

FROM kun otetaan huomioon (1) on nolla:MC = P ∙ AC- K∙ SW = 0.

Näyttelyn tuloksena saimme siis: RC ≠ 0, MC= 0. Tämä tarkoittaa, että päävektori on ekvivalentti redusointikeskuksen läpi kulkevalle resultantille, eli:

Kollineaaristen voimien resultantti on itseisarvoltaan yhtä suuri kuin niiden summa, ja sen toimintalinja jakaa niiden käyttöpisteitä yhdistävän segmentin, kääntäen verrannollinen näiden voimien sisäisiin moduuleihin.

Huomaa, että pisteen sijainti FROM ei muutu, jos voimat R Ja K kääntyä kulmastaα . Piste FROM, jolla on tämä ominaisuus, kutsutaan yhdensuuntaisten voimien keskipiste.

2. Kahden hengen järjestelmä antikollineaarinen eikä voimien moduulissa ole yhtä suuri. Voi voimat P Ja K, sovelletaan kohdissa MUTTA Ja SISÄÄN, yhdensuuntainen, suunnattu vastakkaisiin suuntiin ja eri moduuli (kuva 1, b).

Valitaan piste vertailukeskukseksi FROM, joka silti täyttää suhteen (1) ja sijaitsee samalla suoralla, mutta segmentin ulkopuolella AB.

Tämän järjestelmän päävektori RC = P + K modulo on nyt yhtä suuri kuin vektorien moduulien välinen ero: RC = K - P.

Päähetki keskustasta FROM on edelleen nolla:MC = P ∙ AC- K∙ SW= 0, niin

Tuloksena antikollineaarinen ja voimat, jotka eivät ole yhtä suuret itseisarvoltaan, ovat yhtä suuret kuin niiden ero, on suunnattu suurempaa voimaa kohti, ja sen toimintalinja jakaa niiden kohdistamispisteitä yhdistävän segmentin, kääntäen verrannollinen näiden voimien moduuleihin ulkoisesti.

Kuva 1

3. Kahden hengen järjestelmä antikollineaarinen ja voimat ovat yhtä suuret moduulissa. Otetaan edellinen vähennystapaus alkuperäiseksi. Laitetaan virta kuntoon R, ja voimaa K yritetään modulo pakottaa R.

Sitten klo K → R kaavassa (1) suhde AC/SW → 1. Tämä tarkoittaa sitä AC → SW, eli etäisyys AC →∞ .

Tässä tapauksessa päävektorin moduuli RC → 0, ja päämomentin moduuli ei riipu pelkistyskeskuksen sijainnista ja pysyy samana kuin alkuperäinen arvo:

MC = P ∙ AC- K∙ SW = P ∙ ( AC- SW) =P ∙ MUTTAB.

Siten rajassa olemme saaneet voimajärjestelmän, jolle RC = 0, MC≠ 0, ja pelkistyskeskus poistetaan äärettömään, jota ei voida korvata resultantilla. Tässä järjestelmässä ei ole vaikeaa löytää paria voimia, joten voimaparilla ei ole resultanttia.

Yhdensuuntaisten voimien järjestelmän keskus.

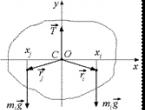
Harkitse järjestelmää n voimat Pi, sovelletaan kohdissaA i (x i , y i , z i) ja yhdensuuntainen akselin kanssaOv vektorin kanssa l(Kuva 2).

Jos suljemme etukäteen pois tapauksen, jossa järjestelmä vastaa voimaparia, ei ole vaikeaa todistaa edellisen kappaleen perusteella sen resultantin olemassaolo.R.

Määritä keskuksen koordinaatitC(x c, y c, z c) rinnakkaiset voimat eli tämän järjestelmän resultantin sovelluspisteen koordinaatit.

Tätä tarkoitusta varten käytämme Varignonin lausetta, jonka perusteella:

M0 (R) = Σ M0(Pi).

Kuva 2

Voiman vektori-momentti voidaan esittää ristitulona, joten:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r i× Pi ).

Olettaen että R = R v ∙ l, mutta Pi = P vi ∙ l ja käyttämällä vektoritulon ominaisuuksia, saamme:

rc × R v ∙ l = Σ ( r i × P vi ∙ l),

rc ∙ R v × l = Σ ( r i ∙ P vi × l) = Σ ( r i ∙ P vi ) × l,

tai:

[ r c R v - Σ ( r i P vi )] × l= 0.

Viimeinen lauseke on voimassa vain, jos hakasulkeissa oleva lauseke on nolla. Siksi indeksi jätetään poisvja ottaen huomioon, että tuloksenaR = Σ Pi , täältä saamme:

rc = (Σ Pi r i )/(Σ Pi ).

Projisoimalla viimeinen vektoriyhtälö koordinaattiakselille saadaan haluttu rinnakkaisten voimien keskipisteen koordinaattien ilmaisu:

x c = (Σ Pi x i)/(Σ Pi );

yc = (Σ Pi y i )/(Σ Pi );(2)

z c = (Σ Pi z i )/(Σ Pi ).

Kehon painopiste

Homogeenisen kappaleen painopisteiden koordinaatit.

Harkitse jäykkää kehon punnitusta P ja äänenvoimakkuus V koordinaattijärjestelmässä Oxyz, jossa akselit x Ja y liittyy maan pintaan ja akseliin z suunnattu zeniittiin.

Jos jaamme kehon alkeellisiin osiin, joilla on tilavuus∆ V i , silloin vetovoima vaikuttaa sen jokaiseen osaan∆ Pisuunnattu kohti maan keskustaa. Oletetaan, että kehon mitat ovat paljon pienemmät kuin Maan mitat, niin kehon perusosiin kohdistuvaa voimajärjestelmää voidaan pitää ei suppenevana, vaan yhdensuuntaisena (kuva 3), ja kaikki johtopäätökset edellisen luvun kohdat soveltuvat siihen.

Kuva 3

Määritelmä . Jäykän kappaleen painopiste on tämän kappaleen perusosien yhdensuuntaisten painovoiman keskipiste.

Muista tuo tietty painovoima kehon perusosaa kutsutaan sen painosuhteeksi∆ Piäänenvoimakkuuteen ∆ V i : γ i = ∆ Pi/ ∆ V i . Homogeeniselle kappaleelle tämä arvo on vakio:γ i = γ = P/ V.

Korvataan (2) ∆ Pi = γ i ∙∆ V i sijasta Pi, kun otetaan huomioon viimeinen huomautus ja vähennetään osoittajaa ja nimittäjääg, saamme lausekkeet homogeenisen kappaleen painopisteen koordinaateille:

x c = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

yc = (Σ ∆ Vi∙ y i )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Useat lauseet ovat hyödyllisiä painopisteen määrittämisessä.

1) Jos homogeenisella kappaleella on symmetriataso, niin sen painopiste on tässä tasossa.

Jos akselit X Ja klo sijoitetaan tähän symmetriatasoon, sitten jokaiselle pisteelle, jossa on koordinaatit. ja koordinoida kohdan (3) mukaan on nolla, koska yhteensä kaikki vastakkaiset termit eliminoidaan pareittain. Painopiste on siis symmetriatasossa.

2) Jos homogeenisella kappaleella on symmetria-akseli, niin kappaleen painopiste sijaitsee tällä akselilla.

Todellakin, tässä tapauksessa, jos akselizpiirrä symmetria-akselia pitkin jokaiselle pisteelle koordinaatteineenvoit löytää pisteen koordinaatteilla ja koordinaatit ja laskettu kaavoilla (3) on yhtä suuri kuin nolla.

Kolmas lause todistetaan samalla tavalla.

3) Jos homogeenisella kappaleella on symmetriakeskus, niin kappaleen painopiste sijaitsee tässä pisteessä.

Ja vielä muutama huomio.

Ensimmäinen. Jos ruumis voidaan jakaa osiin, joiden paino ja painopisteen sijainti tunnetaan, ei jokaista pistettä tarvitse ottaa huomioon, vaan kaavoissa (3) Pi – määritetään kyseisen osan painona jasen painopisteen koordinaatteina.

Toinen. Jos runko on homogeeninen, niin sen erillisen osan paino, missä on sen materiaalin ominaispaino, josta runko on valmistettu, ja Vi - tämän kehon osan tilavuus. Ja kaavat (3) saavat kätevämmän muodon. Esimerkiksi,

Ja vastaavasti missä - koko kehon tilavuus.

Kolmas huomautus. Anna vartalon näyttää ohuelta levyltä, jolla on alue F ja paksuus t makaa lentokoneessa Oxy. Korvataan kohtaan (3)∆ V i =t ∙ ∆F i , saamme homogeenisen levyn painopisteen koordinaatit:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

yc = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z i ) / (Σ ∆ F i).

missä – yksittäisten levyjen painopisteen koordinaatit;on kehon kokonaispinta-ala.

Neljäs huomautus. Runkoon ohuen kaarevan tangon muodossa, jonka pituus on L poikkileikkausalalla a alkeistilavuus∆ V i = a ∙∆ L i , siksi ohuen kaarevan sauvan painopisteen koordinaatit tulee olemaan yhtä suuri:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

yc = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

missä – painopisteen koordinaatiti-th osa; .

Huomaa, että määritelmän mukaan painopiste on geometrinen piste; se voi olla myös tietyn kappaleen rajojen ulkopuolella (esimerkiksi renkaassa).

Huomautus.

Tässä kurssin osassa emme tee eroa painovoiman, painovoiman ja ruumiinpainon välillä. Todellisuudessa painovoima on ero Maan painovoiman ja sen pyörimisen aiheuttaman keskipakovoiman välillä.

Epähomogeenisten kappaleiden painopisteiden koordinaatit.

Painopisteen koordinaatit epähomogeeninen kiinteä aine(Kuva 4) valitussa vertailujärjestelmässä määritellään seuraavasti:

Kuva 4

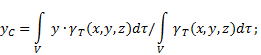
missä - paino ruumiintilavuusyksikköä kohti (ominaispaino)

- koko kehon paino.

epätasainen pinta(Kuva 5), sitten painopisteen koordinaatit valitussa vertailujärjestelmässä määritetään seuraavasti:

Kuva 5

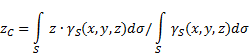
missä - paino kehon pinta-alayksikköä kohti

- koko kehon paino.

Jos kiinteä on heterogeeninen linja(Kuva 6), sitten painopisteen koordinaatit valitussa vertailujärjestelmässä määritetään seuraavasti:

Kuva 6

missä - kehon pituuden yksikköpaino,

Koko kehon paino.

Painopisteen koordinaattien määritysmenetelmät.

Edellä saatujen yleisten kaavojen perusteella on mahdollista osoittaa erityisiä menetelmiä määrittää kappaleiden painopisteiden koordinaatit.

Kuva 7

2. Halkaisu. Runko on jaettu äärelliseen määrään osia (kuva 8), joista jokaiselle tunnetaan painopisteen sijainti ja pinta-ala.

Kuva 8

S \u003d S 1 + S 2.

3.Negatiivisten alueiden menetelmä. Erityinen osiointimenetelmän tapaus (kuva 9). Se koskee kappaleita, joissa on aukko, jos kappaleen painopisteet ilman leikkausta ja leikkausta tunnetaan. Levyn muodossa olevaa runkoa, jossa on aukko, edustaa kiinteän levyn (ilman aukkoa) yhdistelmä, jossa on alue S1 ja leikatun osan alue S2.

Kuva 9

S \u003d S 1 - S 2.

Joidenkin homogeenisten kappaleiden painopisteet.

1) Ympyränkaaren painopiste. Harkitse kaaria AB sädeR keskikulmalla. Symmetrian vuoksi tämän kaaren painopiste sijaitsee akselillaHärkä(Kuva 10).

Kuva 10

Etsitään koordinaatit kaavan mukaan . Voit tehdä tämän valitsemalla kaaresta AB elementti MM ’ pitkä, jonka sijainti määräytyy kulman mukaan. Koordinoi X elementti MM' tahtoa. Korvaa nämä arvot X Ja d l ja kun otetaan huomioon, että integraalia on jatkettava koko kaaren pituudelle, saadaan:

jossa L on kaaren AB pituus, joka on yhtä suuri kuin .

Sieltä lopulta huomaamme, että ympyränkaaren painopiste sijaitsee sen symmetria-akselilla etäisyyden päässä keskustasta Oi tasa-arvoista

missä on kulma mitattuna radiaaneina.

2) Kolmion alueen painopiste. Harkitse tasossa olevaa kolmiota Oxy, jonka kärkikoordinaatit tunnetaan: A i (x i,y i ), (i= 1,2,3). Kolmion murtaminen kapeiksi nauhoiksi sivun suuntaisesti MUTTA 1 MUTTA 2 , tulemme siihen tulokseen, että kolmion painopisteen tulee kuulua mediaaniin MUTTA 3 M 3 (kuvio 11).

Kuva 11

Etenkin mediaanille MUTTA 1 M 1 saamme, koska pisteen koordinaatit M 1 - on pisteiden koordinaattien aritmeettinen keskiarvo MUTTA 2 ja MUTTA 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Siten kolmion painopisteen koordinaatit ovat sen kärkien koordinaattien aritmeettinen keskiarvo:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

3) Pyöreän sektorin alueen painopiste. Tarkastellaan säteisen ympyrän sektoria R keskikulmalla 2α , joka sijaitsee symmetrisesti akselin ympäri Härkä (Kuvio 12) .

Se on selvää y c = 0, ja etäisyys ympyrän keskipisteestä, josta tämä sektori leikataan, sen painopisteeseen voidaan määrittää kaavalla:

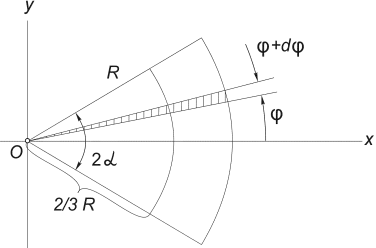
Kuva 12

Helpoin tapa laskea tämä integraali on jakaa integrointialue alkeissektoreiksi kulmalla dφ . Ensimmäisen kertaluvun äärettömiin pieniin määriin asti tällainen sektori voidaan korvata kolmiolla, jonka kanta on yhtä suuri kuin R × dφ ja korkeus R. Tällaisen kolmion pinta-ala dF =(1/2)R 2 ∙ dφ , ja sen painopiste on 2/3 R ylhäältä, joten laitamme kohtaan (5). x = (2/3)R∙ cos. Korvataan kohtaan (5) F= α R 2, saamme:

Viimeisen kaavan avulla laskemme erityisesti etäisyyden painopisteeseen puoliympyrä.

Korvaamalla kohdan (2) α = π /2, saamme: x c = (4 R)/(3 π ) ≅ 0,4 R .

Esimerkki 1Määritetään kuvan 1 mukaisen homogeenisen kappaleen painopiste. 13.

Kuva 13

Ratkaisu.Runko on homogeeninen ja koostuu kahdesta symmetrisestä osasta. Niiden painopisteiden koordinaatit:

Niiden määrät:

Siksi kehon painopisteen koordinaatit

Esimerkki 2 Etsi suorassa kulmassa taivutetun levyn painopiste. Mitat - piirustuksessa (kuva 14).

Kuva 14

Ratkaisu. Painopisteiden koordinaatit:

Neliöt:

Siksi:

Esimerkki 3 Neliömäisellä levyllä cm leikattu neliömäinen reikä katso (kuva 15). Etsi arkin painopiste. Esimerkki 4 Etsi kuvan 1 mukaisen levyn painopisteen sijainti. 16. Mitat on annettu senttimetreinä.

Kuva 16

Ratkaisu. Jaamme levyn kuviin (kuva 17), keskuksia joiden vakavuus on tiedossa.

Näiden kuvien pinta-alat ja niiden painopisteiden koordinaatit:

1) suorakulmio, jonka sivut ovat 30 ja 40 cm,S 1 =30 ∙ 40 = 1200 cm 2 ; x 1= 15 cm; klo 1 \u003d 20 cm.

2) suorakulmainen kolmio, jonka kanta on 50 cm ja korkeus 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; X 2 \u003d 30 + 50 / 3 \u003d 46,7 cm; y 2 =40/3 = 13,3 cm;

3) puoliympyrän ympyrän säde r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; X 3 =4 R /3 π =8,5 cm; klo

Ratkaisu. Muista, että fysiikassa kappaleen tiheysρ ja sen ominaispainogsuhteessa suhteeseen:γ = ρ g , missäg - painovoiman kiihtyvyys. Tällaisen homogeenisen kappaleen massan löytämiseksi sinun on kerrottava tiheys sen tilavuudella.

Kuva 19

Termi "lineaarinen" tai "lineaarinen" tiheys tarkoittaa, että ristikon tangon massan määrittämiseksi lineaarinen tiheys on kerrottava tämän tangon pituudella.

Voit ratkaista ongelman käyttämällä osiointimenetelmää. Esittämällä annettua ristikkoa 6 yksittäisen tangon summana, saamme:

missäL i pituusi - tilan sauva jax i , y i - sen painopisteen koordinaatit.

Näin ollen tietty ristikko voidaan edustaa vain kahden sauvaryhmän yhdistelmällä.

Ensimmäinen ryhmä koostuu sen ensimmäisestä sauvastaL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. Toinen sauvaryhmä koostuu viidestä tangosta, joilleL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

Tilan painopisteen koordinaatit löytyvät kaavasta:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Kysymyksiä itsetutkiskelua varten

Mikä on rinnakkaisten voimien keskipiste?

- Miten rinnakkaisten voimien keskipisteen koordinaatit määritetään?

- Kuinka määrittää yhdensuuntaisten voimien keskipiste, joiden resultantti on nolla?

Mikä on rinnakkaisten voimien keskuksen ominaisuus?

- Millä kaavoilla lasketaan rinnakkaisten voimien keskipisteen koordinaatit?

Mikä on kehon painopiste?

- Miksi Maan vetovoimat, jotka vaikuttavat kehon pisteeseen, voidaan pitää rinnakkaisten voimien järjestelmänä?

- Kirjoita muistiin kaava epähomogeenisten ja homogeenisten kappaleiden painopisteen sijainnin määrittämiseksi, kaava litteiden osien painopisteen sijainnin määrittämiseksi?

- Kirjoita muistiin kaava yksinkertaisten geometristen muotojen painopisteen sijainnin määrittämiseksi: suorakulmio, kolmio, puolisuunnikkaan ja puoliympyrän?

Mitä kutsutaan alueen staattiseksi momentiksi?

- Anna esimerkki kappaleesta, jonka painopiste sijaitsee kehon ulkopuolella.

- Miten symmetriaominaisuuksia käytetään kappaleiden painopisteiden määrittämiseen?

- Mikä on negatiivisten painojen menetelmän ydin?

Missä ympyränkaaren painopiste sijaitsee?

Kuinka voit löytää graafisesti kolmion painopisteen?

- Kirjoita muistiin kaava, joka määrittää ympyränmuotoisen sektorin painopisteen.

- Johda samanlainen kaava ympyränmuotoiselle segmentille käyttämällä kaavoja, jotka määrittävät kolmion ja ympyränmuotoisen sektorin painopisteet.

- Millä kaavoilla lasketaan homogeenisten kappaleiden, litteiden kuvioiden ja viivojen painopisteiden koordinaatit?

- Mitä kutsutaan litteän hahmon alueen staattiseksi momentiksi suhteessa akseliin, miten se lasketaan ja mikä mitta sillä on?

- Kuinka määrittää alueen painopisteen sijainti, jos sen yksittäisten osien painopisteiden sijainti tiedetään?

- Mitä apulauseita käytetään painopisteen sijainnin määrittämisessä?

Piirrä kaavio järjestelmästä ja merkitse siihen painopiste. Jos löydetty painopiste on objektijärjestelmän ulkopuolella, sait väärän vastauksen. Olet ehkä mitannut etäisyyksiä eri vertailupisteistä. Toista mittaukset.

Esimerkiksi jos lapset istuvat keinussa, painopiste on jossain lasten välissä, ei keinun oikealla tai vasemmalla puolella. Myöskään painopiste ei koskaan ole sama kuin piste, jossa lapsi istuu.
Nämä päättelyt pitävät paikkansa kaksiulotteisessa avaruudessa. Piirrä neliö, joka sopii kaikkiin järjestelmän esineisiin. Painopisteen tulee olla tämän neliön sisällä.

Tarkista matematiikka, jos saat pienen tuloksen. Jos origo on järjestelmän toisessa päässä, pieni tulos asettaa painopisteen lähelle järjestelmän päätä. Tämä voi olla oikea vastaus, mutta useimmissa tapauksissa tällainen tulos viittaa virheeseen. Kun laskit momentteja, kerroitko vastaavat painot ja etäisyydet? Jos kertomisen sijaan lisäät painot ja etäisyydet, saat paljon pienemmän tuloksen.

Korjaa virhe, jos löydät useita painopisteitä. Jokaisella järjestelmällä on vain yksi painopiste. Jos löysit useita painopisteitä, et todennäköisesti laskenut kaikkia hetkiä yhteen. Painopiste on yhtä suuri kuin "kokonais"-momentin suhde "kokonaispainoon". Sinun ei tarvitse jakaa "jokaista" hetkeä "jokaisella" painolla: näin löydät jokaisen esineen sijainnin.

Tarkista viitepiste, jos vastaus eroaa jollakin kokonaisluvulla. Esimerkissämme vastaus on 3,4 m. Oletetaan, että sait vastauksen 0,4 m tai 1,4 m tai jokin muu numero, joka päättyy ".4". Tämä johtuu siitä, että et valinnut vertailupisteeksi laudan vasenta päätä, vaan pisteen, joka sijaitsee oikealla kokonaisluvun verran. Itse asiassa vastauksesi on oikea riippumatta siitä, minkä viitekohdan valitset! Muista vain: vertailupiste on aina paikassa x = 0. Tässä on esimerkki:

Esimerkissämme vertailupiste oli laudan vasemmassa päässä ja havaitsimme, että painopiste on 3,4 m tästä vertailupisteestä.
Jos valitset vertailupisteeksi pisteen, joka sijaitsee 1 m etäisyydellä laudan vasemmasta päästä oikealla, saat vastaukseksi 2,4 m. Eli painopiste on etäisyydellä 2,4 m uudesta vertailupisteestä, joka puolestaan sijaitsee 1 m etäisyydellä laudan vasemmasta päästä. Painopiste on siis etäisyydellä 2,4 + 1 = 3,4 m laudan vasemmasta päästä. Sain vanhan vastauksen!
Huomautus: Kun mittaat etäisyyttä, muista, että etäisyydet "vasemmalle" vertailupisteelle ovat negatiivisia ja "oikea" referenssipisteitä ovat positiivisia.

Mittaa etäisyydet suorilla viivoilla. Oletetaan, että keinussa on kaksi lasta, mutta toinen lapsi on paljon pidempi kuin toinen, tai toinen lapsi roikkuu laudan alla sen sijaan, että istuu sillä. Jätä tämä ero huomioimatta ja mittaa etäisyydet laudan suoraa pitkin. Etäisyyksien mittaaminen kulmissa johtaa läheisiin, mutta ei aivan tarkkoihin tuloksiin.

Jos kyseessä on kääntölautaongelma, muista, että painopiste on laudan oikean ja vasemman pään välissä. Myöhemmin opit laskemaan monimutkaisempien kaksiulotteisten järjestelmien painopisteen.

kirjoittaja: Otetaan mielivaltainen muotokappale. Onko mahdollista ripustaa se langan päälle niin, että se pysyy ripustamisen jälkeen asennossaan (eli ei lähde kääntymään), kun minkä tahansa alkusuuntaus (kuva 27.1)?

Toisin sanoen, onko olemassa sellaista pistettä, johon nähden kehon eri osiin vaikuttavien painovoimavoimien momenttien summa olisi nolla minkä tahansa kehon suunta avaruudessa?

Lukija: Kyllä, luulen niin. Tällaista kohtaa kutsutaan kehon painopiste.

Todiste. Yksinkertaisuuden vuoksi harkitse kappaletta, joka on mielivaltaisen muotoisen litteän levyn muodossa, joka on mielivaltaisesti suunnattu avaruuteen (kuva 27.2). Ota koordinaattijärjestelmä X 0klo jonka origo on massakeskipisteessä - piste FROM, sitten x C = 0, osoitteessa C = 0.

Edustamme tätä kehoa suuren määrän pistemassojen kokoelmana m i, joiden kunkin sijainnin antaa sädevektori .

Massakeskuksen ja koordinaatin määritelmän mukaan x C = .

Koska meidän koordinaattijärjestelmässämme x C= 0, sitten . Kerrotaan tämä yhtälö g ja saada

Kuten kuvasta näkyy. 27.2, | x i| on voiman olkapää. Ja jos x i> 0, sitten voimamomentti M i> 0 ja jos x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i voiman hetki tulee olemaan M i = m i gx i . Sitten yhtäläisyys (1) vastaa , Jossa M i on painovoiman hetki. Ja tämä tarkoittaa, että kehon mielivaltaisella suunnalla kehoon vaikuttavien painovoimavoimien momenttien summa on yhtä suuri kuin nolla suhteessa sen massakeskukseen.

Jotta harkitsemamme keho olisi tasapainossa, siihen on sovellettava jossakin pisteessä FROM vahvuus T = mg osoittaa pystysuoraan ylöspäin. Tämän voiman hetki pisteestä FROM on yhtä kuin nolla.

Koska päättelymme ei millään tavalla riippunut siitä, kuinka tarkkaan keho on avaruudessa suunnattu, osoitimme, että painopiste on sama kuin massakeskipiste, mikä oli todistettava.

Ongelma 27.1. Etsi painottoman pituisen sauvan painopiste l, jonka päihin on kiinnitetty kaksi pistemassaa T 1 ja T 2 .

T 1 T 2 l	Ratkaisu. Emme etsi painopistettä, vaan massakeskusta (koska ne ovat yksi ja sama). Esittelemme akselin X(Kuva 27.3). Riisi. 27.3
x C =?

Vastaus: pois massasta T 1 .

LOPETTAA! Päätä itse: B1-B3.

Lausunto 1 . Jos homogeenisella litteällä kappaleella on symmetria-akseli, painopiste on tällä akselilla.

Todellakin, mille tahansa pistemassalle m i, joka sijaitsee symmetria-akselin oikealla puolella, on sama pistemassa symmetrisesti ensimmäiseen nähden (kuva 27.4). Tässä tapauksessa voimien momenttien summa.

Koska koko kappale voidaan esittää jaettuna samanlaisiin pistepareihin, painovoiman kokonaismomentti suhteessa mihin tahansa symmetria-akselilla olevaan pisteeseen on nolla, mikä tarkoittaa, että myös kappaleen painopiste sijaitsee tällä akselilla. Tästä seuraa tärkeä johtopäätös: jos kappaleessa on useita symmetriaakseleita, niin painopiste on näiden akselien leikkauskohdassa(Kuva 27.5).

Riisi. 27.5

Lausuma 2. Jos kaksi kappaletta, joilla on massoja T 1 ja T 2 on yhdistetty yhdeksi, silloin tällaisen kappaleen painopiste on suoralla linjalla, joka yhdistää ensimmäisen ja toisen kappaleen painopisteet (kuva 27.6).

Riisi. 27.6 Riisi. 27.7

Todiste. Järjestetään komposiittikappale siten, että kappaleiden painopisteitä yhdistävä segmentti on pystysuora. Sitten ensimmäisen kappaleen painovoimamomenttien summa pisteen suhteen FROM 1 on yhtä suuri kuin nolla ja toisen kappaleen painovoimamomenttien summa pisteen ympärillä FROM 2 on nolla (kuva 27.7).

huomaa, että olkapää minkä tahansa pistemassan painovoima t i sama minkä tahansa janan pisteen suhteen FROM 1 FROM 2, ja siten painovoiman suhteessa mihin tahansa segmentillä olevaan pisteeseen FROM 1 FROM 2 ovat samat. Siksi koko kehon painovoima on nolla suhteessa mihin tahansa segmentin pisteeseen FROM 1 FROM 2. Siten komposiittikappaleen painopiste sijaitsee segmentillä FROM 1 FROM 2 .

Lause 2 sisältää tärkeän käytännön johtopäätöksen, joka on selkeästi muotoiltu ohjeiden muodossa.

ohje,

kuinka löytää jäykän kappaleen painopiste, jos se voidaan rikkoa

osiin, joiden jokaisen painopisteiden sijainti tunnetaan

1. Korvaa jokainen osa massalla, joka sijaitsee kyseisen osan painopisteessä.

2. Etsi Painovoiman keskipiste(ja tämä on sama kuin painopiste) tuloksena olevasta pistemassajärjestelmästä valitsemalla sopiva koordinaattijärjestelmä X 0klo, kaavojen mukaan:

Todellakin, sijoitetaan yhdistelmäkappale siten, että segmentti FROM 1 FROM 2 oli vaakasuora, ja ripustamme sen kierteisiin kohdissa FROM 1 ja FROM 2 (kuva 27.8, mutta). On selvää, että keho on tasapainossa. Ja tämä tasapaino ei häiriinny, jos korvaamme jokaisen kappaleen pistemassoilla T 1 ja T 2 (kuva 27.8, b).

Riisi. 27.8

LOPETTAA! Päätä itse: C3.

Ongelma 27.2. Massapallot asetetaan tasasivuisen kolmion kahteen kärkeen T joka. Kolmas huippu sisältää pallon, jonka massa on 2 T(Kuva 27.9, mutta). Kolmion puoli mutta. Määritä tämän järjestelmän painopiste.

T 2T mutta	Riisi. 27.9
x C = ? osoitteessa C = ?

Ratkaisu. Esittelemme koordinaattijärjestelmän X 0klo(Kuva 27.9, b). Sitten

Vastaus: x C = mutta/2; ; painopiste on puolessa korkeudesta ILMOITUS.