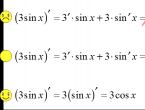Null functions. Let's find the zeros of the function

What are function zeros? The answer is quite simple - this is a mathematical term, which means the domain of definition of a given function, in which its value is zero. Function zeros are also called. The easiest way to explain what function zeros are is with a few simple examples.

Examples

Let's consider the simple equation y=x+3. Since the zero of a function is the value of the argument at which y acquired a zero value, we substitute 0 on the left side of the equation:

In this case, -3 is the desired zero. For a given function there is only one root of the equation, but this is not always the case.

Let's look at another example:

Let's substitute 0 on the left side of the equation, as in the previous example:

Obviously, in this case there will be two zeros of the function: x=3 and x=-3. If the equation had a third-degree argument, there would be three zeros. A simple conclusion can be drawn that the number of roots of the polynomial corresponds to the maximum degree of the argument in the equation. However, many functions, for example y = x 3, at first glance contradict this statement. Logic and common sense dictate that this function has only one zero - at the point x=0. But in fact there are three roots, they just all coincide. If you solve the equation in complex form, this becomes obvious. x=0 in this case, a root whose multiplicity is 3. In the previous example, the zeros did not coincide, therefore they had a multiplicity of 1.

Determination algorithm

From the presented examples you can see how to determine the zeros of a function. The algorithm is always the same:

1. Write a function.
2. Substitute y or f(x)=0.
3. Solve the resulting equation.

The difficulty of the last point depends on the degree of the argument of the equation. When solving equations of high degrees, it is especially important to remember that the number of roots of the equation is equal to the maximum degree of the argument. This is especially true for trigonometric equations, where dividing both sides by sine or cosine leads to the loss of roots.

Equations of arbitrary degree are easiest to solve using Horner's method, which was developed specifically for finding the zeros of an arbitrary polynomial.

The value of zeros of functions can be either negative or positive, real or in the complex plane, singular or multiple. Or there may be no roots to the equation. For example, the function y=8 will not acquire a zero value for any x, because it does not depend on this variable.

The equation y=x 2 -16 has two roots, and both lie in the complex plane: x 1 =4i, x 2 =-4i.

Common mistakes

A common mistake made by schoolchildren who have not yet fully understood what zeros of a function are is replacing the argument (x) with zero, rather than the value (y) of the function. They confidently substitute x=0 into the equation and, based on this, find y. But this is the wrong approach.

Another mistake, as already mentioned, is reduction by sine or cosine in a trigonometric equation, which is why one or more zeros of the function are lost. This does not mean that nothing can be reduced in such equations, but in further calculations it is necessary to take into account these “lost” factors.

Graphical representation

You can understand what the zeros of a function are using mathematical programs such as Maple. You can build a graph in it by specifying the desired number of points and the desired scale. Those points at which the graph intersects the OX axis are the desired zeros. This is one of the fastest ways to find the roots of a polynomial, especially if its order is higher than third. So if there is a need to regularly perform mathematical calculations, find the roots of polynomials of arbitrary degrees, build graphs, Maple or a similar program will be simply indispensable for carrying out and checking calculations.

Content:

The zero of a function is the value of x at which the value of the function is zero. Typically, finding the zeros of a function is done by solving a polynomial equation, such as x 2 + 4x +3 = 0. Here are several ways to find the zeros of a function.

Steps

1 Factorization

1. 1 Write the equation so it looks something like x 2 + 5x + 4. Start with a higher order term (such as x 2) and then work down to a free term (a constant without a variable; a number). Equate the resulting expression to 0.
   • Polynomials (equations) written correctly:
     • x 2 + 5x + 6 = 0
     • x 2 - 2x – 3 = 0
   • Polynomials (equations) written incorrectly:
     • 5x + 6 = -x 2
     • x 2 = 2x + 3
2. 2 a", "b", "c". This will simplify the factorization problem. Write the equation in this format: a x 2 ± b x ± c = 0. Now find a, b, c from the equation given to you. Here are some examples:
   • x 2 + 5x + 6 = 0
     • a
     • b = 5
     • c = 6
   • x 2 - 2x – 3 = 0
     • a= 1 (there is no coefficient before “x”, so coefficient = 1)
     • b = -2
     • c = -3
3. 3 Write down all pairs of coefficient factors " With". A pair of factors of a given number are two numbers that, when multiplied, give that number. Pay special attention to negative numbers. Two negative numbers, when multiplied, give a positive number. The order of the multiplication does not matter ("1 x 4" is the same as "4 x 1").
   • Equation: x 2 + 5x + 6 = 0
   • Multiplier pairs 6, or c:
     • 1 x 6 = 6
     • -1 x -6 = 6
     • 2 x 3 = 6
     • -2 x -3 = 6
4. 4 Find a pair of factors whose sum is " b" . Look at the meaning b and find which of the pairs, when summed, will give this number.
   • b = 5
   • A pair of multipliers whose sum is 5 is 2 and 3
     • 2 + 3 = 5
5. 5 From this pair of factors, make 2 binomials and combine them into a binomial. A binomial is the product of binomials of the form (x ± number)(x ± number). How do you know which sign (plus or minus) to choose? Just look at the sign of the numbers from a pair of factors: a positive number is a plus sign, a negative number is a minus sign. Here are a couple of factors with which we made the binomial:
   • (x + 2)(x + 3) = 0
6. 6 Solve each binomial by moving the unknown to the other side of the equation. Equate each binomial to 0: (x + 2) = 0 and (x + 3) = 0, and then solve the equation:
   • (x + 2) = 0; x = -2
   • (x + 3) = 0; x = -3
7. 7 These are the zeros of the function.

2 Solving a quadratic equation

1. 1 The quadratic equation looks like this:
2. 2 Denote the coefficients in your equation by " a", "b", "c". This will simplify the problem of solving the equation. Write the equation in this format: a x 2 ± b x ± c = 0.
3. 3 Now find a, b, c from the equation given to you.
4. 4 Solve the equation. To solve a quadratic equation, you need to know the formula for solving such an equation. Everything else is just substitution and calculation.
   • Another option for solving a quadratic equation is a perfect square. Some people consider this method simpler than solving by formula.
5. 5 The result of solving a quadratic equation using the formula will be the “zeros” of the function that you are looking for. The formula gives the answer in the form of two numbers, which are the solution (zeros) of this function.

3 Graph of a quadratic equation

1. 1 Graph the function. The function is written as x 2 + 8x + 12 = 0.
2. 2 Find the x-intercepts. These two points will be the zeros of the function.
3. 3 Use the graph as a way to check, not as a way to solve an equation. If you are plotting to show the zeros of a function, use this to double check your results.

• You can check your calculations by substituting the solutions found into the initial equation. If the equation is equal to zero, then the solutions are correct.

Function zeros are the argument values ​​at which the function is equal to zero.

To find the zeros of the function given by the formula y=f(x), you need to solve the equation f(x)=0.

If the equation has no roots, the function has no zeros.

Examples.

1) Find the zeros of the linear function y=3x+15.

To find the zeros of the function, solve the equation 3x+15=0.

Thus, the zero of the function y=3x+15 is x= -5.

Answer: x= -5.

2) Find the zeros of the quadratic function f(x)=x²-7x+12.

To find the zeros of the function, solve the quadratic equation

Its roots x1=3 and x2=4 are zeros of this function.

Answer: x=3; x=4.

Instructions

1. The zero of a function is the value of the argument x at which the value of the function is equal to zero. However, only those arguments that are within the scope of the definition of the function under study can be zeros. That is, there are a lot of values ​​for which the function f(x) is useful. 2. Write down the given function and equate it to zero, say f(x) = 2x?+5x+2 = 0. Solve the resulting equation and find its real roots. The roots of a quadratic equation are calculated with support for finding the discriminant. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Thus, in this case, two roots of the quadratic equation are obtained, corresponding to the arguments of the initial function f(x). 3. Check all detected x values ​​for belonging to the domain of definition of the given function. Find out the OOF, to do this, check the initial expression for the presence of even roots of the form?f (x), for the presence of fractions in the function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions. 4. When considering a function with an expression under a root of an even degree, take as the domain of definition all the arguments x, the values ​​of which do not turn the radical expression into a negative number (on the contrary, the function does not make sense). Check whether the detected zeros of the function fall within a certain range of acceptable x values. 5. The denominator of the fraction cannot go to zero; therefore, exclude those arguments x that lead to such a result. For logarithmic quantities, only those values ​​of the argument should be considered for which the expression itself is greater than zero. Zeros of the function that turn the sublogarithmic expression into zero or a negative number must be discarded from the final result. Note! When finding the roots of an equation, extra roots may appear. This is easy to check: just substitute the resulting value of the argument into the function and make sure whether the function turns to zero. Helpful advice Occasionally a function is not expressed in an obvious way through its argument, then it is easy to know what this function is. An example of this is the equation of a circle.

Function zeros The abscissa value at which the value of the function is equal to zero is called.

If a function is given by its equation, then the zeros of the function will be the solutions to the equation. If a graph of a function is given, then the zeros of the function are the values ​​at which the graph intersects the x-axis.

Algorithm interval method simple and straightforward:

1) Find domain of a function.

2) Find function zeros(points of intersection of the graph with the x-axis).

3) Most tasks will require a drawing. We draw an axis and plot the breakpoints (if any) on it, as well as the zeros of the function (if there are any). We determine the signs of the function on intervals that are included in the domain of definition.

You can jot down the points, however, the algorithm will very quickly remember even a full kettle. Everything here is transparent and logical.

Let's start with a common quadratic function:

Example 1

Find the intervals of constant sign of the function.

Solution:

1) The function is defined and continuous on the entire number line. Thus, break points and there are no “bad” gaps.

2) Find the zeros of the function. To do this you need to solve the equation. In this case:

The discriminant is positive, which means the equation has two real roots:

3) We plot all the found points on the number axis:

In the article Function Domain I made similar drawings schematically, but now for greater clarity of presentation I will scale them (with the exception of clinical cases). In the same lesson, we learned how to figure out the signs of a function on intervals - we can analyze the location of a parabola. In this case, the branches of the parabola are directed upward, therefore, at intervals the function will be positive: . The bottom of the parabola sits on the interval below the x-axis, and the function here is negative: .

Well, many readers imagine a parabola. But what if the function is more complex? For example, . A significant part of the audience will already find it difficult to say what the graph of this function fundamentally looks like. And this, so to speak, is only a minimal complication.

However, a universal method works in both simple and complex cases:

Let us consider a function continuous on a certain interval, the graph of which does not intersect the axis on this interval. Then:

If the function positive at any point in the interval, then it is positive and IN ALL points of this interval;

If the function negative at any point in the interval, then it is negative and IN ALL points of this interval.

Use a little imagination: if there are no break points in the interval, and the graph does not cross the x-axis, then it cannot, with the wave of a magic wand, jump from the lower half-plane to the upper half-plane (or vice versa). Therefore, the sign of the function on such an interval can be easily determined from a single point.

Let's do a little experiment. Imagine that you have no idea what the graph of a function looks like and you need to find her intervals of sign constancy (by the way, if you really don’t know, draw the long-suffering prima donna =)).

1) Take an arbitrary point of the interval. From a computational point of view, it is easiest to take . We substitute it into our function:

Therefore, the function is positive and in each point of the interval.

2) We take an arbitrary point of the interval, here, for convenience, zero is beyond competition.

We perform the substitution again:

This means that the function is negative and in each point of the interval.

3) And finally, we process the simplest point of the interval:

Therefore the function is positive in each point of the interval.

Completed substitutions and calculations are almost always easy to do orally, but as a last resort there is a draft.

We record the results obtained on the numerical axis:

Yes, you have no idea about the parabola, but you can definitely say that on the intervals graph of a function is located ABOVE the axis, and on the interval - BELOW this axis.

Answer:

If ;
, If .

A whole range of “satellite” problems are solved in the same way, here are some of them:

.

We carry out similar actions and give an answer .

Solve quadratic inequality .

We carry out similar actions and give an answer.

Finddomain functions .

We carry out similar actions and give an answer.

The interval method works in the most primitive cases, for example, for the function. Here the straight line intersects the x-axis at point , while to the left of this point (graph below the axis), and to the right (graph above the axis). However, for those in the tank, the problem can be solved using the interval method.

Can a function be positive or negative on the entire number line? Of course, in the article Function Domain We looked at typical examples. In particular, they found that (a parabola lying entirely in the upper half-plane). The interval method works here too! We consider a single interval, take the most convenient point from it and perform the substitution: . This means that the function is positive at every point of the interval.

The mathematical representation of a function clearly shows how one quantity completely determines the value of another quantity. Traditionally, numerical functions are considered that assign one number to another. The zero of a function is usually the value of the argument at which the function becomes zero.

Instructions

1. In order to detect the zeros of a function, you need to equate its right side to zero and solve the resulting equation. Let's imagine you are given a function f(x)=x-5.

2. To find the zeros of this function, let’s take and equate its right side to zero: x-5=0.

3. Having solved this equation, we find that x=5 and this value of the argument will be the zero of the function. That is, when the argument value is 5, the function f(x) becomes zero.

Under the view functions in mathematics we understand the connection between the elements of sets. To put it more correctly, this is a “law” according to which the entire element of one set (called the domain of definition) is associated with a certain element of another set (called the domain of values).

You will need

• Knowledge of algebra and mathematical review.

Instructions

1. Values functions This is a certain area from which a function can take values. Let's say the range of values functions f(x)=|x| from 0 to infinity. In order to discover meaning functions at a certain point you need to substitute the argument functions its numerical equivalent, the resulting number will be meaning m functions. Let the function f(x)=|x| – 10 + 4x. Let's find out meaning functions at point x=-2. Let's replace x with the number -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. That is meaning functions at point -2 is equal to -16.

Note!
Before looking for the value of a function at a point, make sure that it is within the domain of the function.

Helpful advice
A similar method allows one to discover the meaning of the function of several arguments. The difference is that instead of one number you will need to substitute several - according to the number of arguments of the function.

The function represents the established connection between the variable y and the variable x. Moreover, all the values ​​of x, called the argument, correspond to the exceptional value of y - the function. In graphical form, a function is depicted on a Cartesian coordinate system in the form of a graph. The points of intersection of the graph with the abscissa axis, on which the arguments x are plotted, are called zeros of the function. Finding acceptable zeros is one of the tasks of finding a given function. In this case, all permissible values ​​of the independent variable x that form the domain of definition of the function (DOF) are taken into account.

Instructions

1. The zero of a function is the value of the argument x at which the value of the function is equal to zero. However, only those arguments that are within the scope of the definition of the function under study can be zeros. That is, there are a lot of values ​​for which the function f(x) is useful.

2. Write down the given function and equate it to zero, say f(x) = 2x?+5x+2 = 0. Solve the resulting equation and find its real roots. The roots of a quadratic equation are calculated with support for finding the discriminant. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Thus, in this case, two roots of the quadratic equation are obtained, corresponding to the arguments of the initial function f(x).

3. Check all detected x values ​​for belonging to the domain of definition of the given function. Find out the OOF, to do this, check the initial expression for the presence of even roots of the form?f (x), for the presence of fractions in the function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions.

4. When considering a function with an expression under the root of an even degree, take as the domain of definition all the arguments x, the values ​​of which do not turn the radical expression into a negative number (on the contrary, the function does not make sense). Check whether the detected zeros of the function fall within a certain range of acceptable x values.

5. The denominator of the fraction cannot go to zero; therefore, exclude those arguments x that lead to such a result. For logarithmic quantities, only those values ​​of the argument should be considered for which the expression itself is greater than zero. Zeros of the function that turn the sublogarithmic expression into zero or a negative number must be discarded from the final result.

Note!
When finding the roots of an equation, extra roots may appear. This is easy to check: just substitute the resulting value of the argument into the function and make sure whether the function turns to zero.

Helpful advice
Occasionally a function is not expressed in an obvious way through its argument, then it is easy to know what this function is. An example of this is the equation of a circle.