Today we will talk about execution order mathematical actions. What actions should you take first? Addition and subtraction, or multiplication and division. It’s strange, but our children have problems solving seemingly elementary expressions.

So, remember that the expressions in parentheses are evaluated first

38 – (10 + 6) = 22 ;

Procedure:

1) in brackets: 10 + 6 = 16;

2) subtraction: 38 – 16 = 22.

If an expression without parentheses involves only addition and subtraction, or only multiplication and division, then the operations are performed in order from left to right.

10 ÷ 2 × 4 = 20;

Procedure:

1) from left to right, division first: 10 ÷ 2 = 5;

2) multiplication: 5 × 4 = 20;

10 + 4 – 3 = 11, i.e.:

1) 10 + 4 = 14 ;

2) 14 – 3 = 11 .

If in an expression without parentheses there is not only addition and subtraction, but also multiplication or division, then the actions are performed in order from left to right, but multiplication and division have priority, they are performed first, followed by addition and subtraction.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Procedure:

1) 18 ÷ 2 = 9;

2) 2 × 3 = 6;

3) 12 ÷ 3 = 4;

4) 9 – 6 = 3; those. from left to right – the result of the first action minus the result of the second;

5) 3 + 4 = 7; those. the result of the fourth action plus the result of the third;

If an expression contains parentheses, then the expressions in the parentheses are performed first, then multiplication and division, and only then addition and subtraction.

30 + 6 × (13 – 9) = 54, i.e.:

1) expression in brackets: 13 – 9 = 4;

2) multiplication: 6 × 4 = 24;

3) addition: 30 + 24 = 54;

So, let's summarize. Before you begin the calculation, you need to analyze the expression: whether it contains parentheses and what actions it contains. After this, proceed with calculations in the following order:

1) actions enclosed in brackets;

2) multiplication and division;

3) addition and subtraction.

If you want to receive announcements of our articles, subscribe to the newsletter ““.

The original source is located. Alpha stands for real number. The equal sign in the above expressions indicates that if you add a number or infinity to infinity, nothing will change, the result will be the same infinity. If we take the infinite set of natural numbers as an example, then the considered examples can be represented in this form:

To clearly prove that they were right, mathematicians came up with many different methods. Personally, I look at all these methods as shamans dancing with tambourines. Essentially, they all boil down to the fact that either some of the rooms are unoccupied and new guests are moving in, or that some of the visitors are thrown out into the corridor to make room for guests (very humanly). I presented my view on such decisions in the form of a fantasy story about the Blonde. What is my reasoning based on? Relocating an infinite number of visitors takes an infinite amount of time. After we have vacated the first room for a guest, one of the visitors will always walk along the corridor from his room to the next one until the end of time. Of course, the time factor can be stupidly ignored, but this will be in the category of “no law is written for fools.” It all depends on what we are doing: adjusting reality to mathematical theories or vice versa.

What is an “endless hotel”? An infinite hotel is a hotel that always has any number of empty beds, regardless of how many rooms are occupied. If all the rooms in the endless "visitor" corridor are occupied, there is another endless corridor with "guest" rooms. There will be an infinite number of such corridors. Moreover, the “infinite hotel” has an infinite number of floors in an infinite number of buildings on an infinite number of planets in an infinite number of universes created by an infinite number of Gods. Mathematicians are not able to distance themselves from banal everyday problems: there is always only one God-Allah-Buddha, there is only one hotel, there is only one corridor. So mathematicians are trying to juggle the serial numbers of hotel rooms, convincing us that it is possible to “shove in the impossible.”

I will demonstrate the logic of my reasoning to you using the example of an infinite set of natural numbers. First you need to answer a very simple question: how many sets of natural numbers are there - one or many? There is no correct answer to this question, since we invented numbers ourselves; numbers do not exist in Nature. Yes, Nature is great at counting, but for this she uses other mathematical tools that are not familiar to us. I’ll tell you what Nature thinks another time. Since we invented numbers, we ourselves will decide how many sets of natural numbers there are. Let's consider both options, as befits real scientists.

Option one. “Let us be given” one single set of natural numbers, which lies serenely on the shelf. We take this set from the shelf. That's it, there are no other natural numbers left on the shelf and nowhere to take them. We cannot add one to this set, since we already have it. What if you really want to? No problem. We can take one from the set we have already taken and return it to the shelf. After that, we can take one from the shelf and add it to what we have left. As a result, we will again get an infinite set of natural numbers. You can write down all our manipulations like this:

I wrote down the actions in algebraic notation and in set theory notation, with a detailed listing of the elements of the set. The subscript indicates that we have one and only set of natural numbers. It turns out that the set of natural numbers will remain unchanged only if one is subtracted from it and the same unit is added.

Option two. We have many different infinite sets of natural numbers on our shelf. I emphasize - DIFFERENT, despite the fact that they are practically indistinguishable. Let's take one of these sets. Then we take one from another set of natural numbers and add it to the set we have already taken. We can even add two sets of natural numbers. This is what we get:

The subscripts "one" and "two" indicate that these elements belonged to different sets. Yes, if you add one to an infinite set, the result will also be an infinite set, but it will not be the same as the original set. If you add another infinite set to one infinite set, the result is a new infinite set consisting of the elements of the first two sets.

The set of natural numbers is used for counting in the same way as a ruler is for measuring. Now imagine that you added one centimeter to the ruler. This will be a different line, not equal to the original one.

You can accept or not accept my reasoning - it is your own business. But if you ever encounter mathematical problems, think about whether you are following the path of false reasoning trodden by generations of mathematicians. After all, studying mathematics, first of all, forms a stable stereotype of thinking in us, and only then adds to our mental abilities (or, conversely, deprives us of free-thinking).

pozg.ru

Sunday, August 4, 2019

I was finishing a postscript to an article about and saw this wonderful text on Wikipedia:

We read: "... the rich theoretical basis of the mathematics of Babylon did not have a holistic character and was reduced to a set of disparate techniques, devoid of a common system and evidence base."

Wow! How smart we are and how well we can see the shortcomings of others. Is it difficult for us to look at modern mathematics in the same context? Slightly paraphrasing the above text, I personally got the following:

The rich theoretical basis of modern mathematics is not holistic in nature and is reduced to a set of disparate sections, devoid of a common system and evidence base.

I won’t go far to confirm my words - it has a language and conventions that are different from the language and conventions of many other branches of mathematics. The same names in different branches of mathematics can have different meanings. I want to devote a whole series of publications to the most obvious mistakes of modern mathematics. See you soon.

Saturday, August 3, 2019

How to divide a set into subsets? To do this, you need to enter a new unit of measurement that is present in some of the elements of the selected set. Let's look at an example.

May we have plenty A consisting of four people. This set is formed on the basis of “people.” Let us denote the elements of this set by the letter A, the subscript with a number will indicate the serial number of each person in this set. Let's introduce a new unit of measurement "gender" and denote it by the letter b. Since sexual characteristics are inherent in all people, we multiply each element of the set A based on gender b. Notice that our set of “people” has now become a set of “people with gender characteristics.” After this we can divide the sexual characteristics into male bm and women's bw sexual characteristics. Now we can apply a mathematical filter: we select one of these sexual characteristics, no matter which one - male or female. If a person has it, then we multiply it by one, if there is no such sign, we multiply it by zero. And then we use regular school mathematics. Look what happened.

After multiplication, reduction and rearrangement, we ended up with two subsets: the subset of men Bm and a subset of women Bw. Mathematicians reason in approximately the same way when they apply set theory in practice. But they don’t tell us the details, but give us the finished result - “a lot of people consist of a subset of men and a subset of women.” Naturally, you may have a question: how correctly has the mathematics been applied in the transformations outlined above? I dare to assure you that essentially everything was done correctly; it is enough to know the mathematical basis of arithmetic, Boolean algebra and other branches of mathematics. What it is? Some other time I will tell you about this.

As for supersets, you can combine two sets into one superset by selecting the unit of measurement present in the elements of these two sets.

As you can see, units of measurement and ordinary mathematics make set theory a relic of the past. A sign that all is not well with set theory is that mathematicians have come up with their own language and notation for set theory. Mathematicians acted as shamans once did. Only shamans know how to “correctly” apply their “knowledge.” They teach us this “knowledge”.

In conclusion, I want to show you how mathematicians manipulate .

Monday, January 7, 2019

In the fifth century BC, the ancient Greek philosopher Zeno of Elea formulated his famous aporias, the most famous of which is the “Achilles and the Tortoise” aporia. Here's what it sounds like:

Let's say Achilles runs ten times faster than the tortoise and is a thousand steps behind it. During the time it takes Achilles to run this distance, the tortoise will crawl a hundred steps in the same direction. When Achilles runs a hundred steps, the tortoise crawls another ten steps, and so on. The process will continue ad infinitum, Achilles will never catch up with the tortoise.

This reasoning became a logical shock for all subsequent generations. Aristotle, Diogenes, Kant, Hegel, Hilbert... They all considered Zeno's aporia in one way or another. The shock was so strong that " ... discussions continue to this day; the scientific community has not yet been able to come to a common opinion on the essence of paradoxes ... mathematical analysis, set theory, new physical and philosophical approaches were involved in the study of the issue; none of them became a generally accepted solution to the problem..."[Wikipedia, "Zeno's Aporia". Everyone understands that they are being fooled, but no one understands what the deception consists of.

From a mathematical point of view, Zeno in his aporia clearly demonstrated the transition from quantity to . This transition implies application instead of permanent ones. As far as I understand, the mathematical apparatus for using variable units of measurement has either not yet been developed, or it has not been applied to Zeno’s aporia. Applying our usual logic leads us into a trap. We, due to the inertia of thinking, apply constant units of time to the reciprocal value. From a physical point of view, this looks like time slowing down until it stops completely at the moment when Achilles catches up with the turtle. If time stops, Achilles can no longer outrun the tortoise.

If we turn our usual logic around, everything falls into place. Achilles runs at a constant speed. Each subsequent segment of his path is ten times shorter than the previous one. Accordingly, the time spent on overcoming it is ten times less than the previous one. If we apply the concept of “infinity” in this situation, then it would be correct to say “Achilles will catch up with the turtle infinitely quickly.”

How to avoid this logical trap? Remain in constant units of time and do not switch to reciprocal units. In Zeno's language it looks like this:

In the time it takes Achilles to run a thousand steps, the tortoise will crawl a hundred steps in the same direction. During the next time interval equal to the first, Achilles will run another thousand steps, and the tortoise will crawl a hundred steps. Now Achilles is eight hundred steps ahead of the tortoise.

This approach adequately describes reality without any logical paradoxes. But this is not a complete solution to the problem. Einstein’s statement about the irresistibility of the speed of light is very similar to Zeno’s aporia “Achilles and the Tortoise”. We still have to study, rethink and solve this problem. And the solution must be sought not in infinitely large numbers, but in units of measurement.

Another interesting aporia of Zeno tells about a flying arrow:

A flying arrow is motionless, since at every moment of time it is at rest, and since it is at rest at every moment of time, it is always at rest.

In this aporia, the logical paradox is overcome very simply - it is enough to clarify that at each moment of time a flying arrow is at rest at different points in space, which, in fact, is motion. Another point needs to be noted here. From one photograph of a car on the road it is impossible to determine either the fact of its movement or the distance to it. To determine whether a car is moving, you need two photographs taken from the same point at different points in time, but you cannot determine the distance from them. To determine the distance to a car, you need two photographs taken from different points in space at one point in time, but from them you cannot determine the fact of movement (of course, you still need additional data for calculations, trigonometry will help you). What I want to draw special attention to is that two points in time and two points in space are different things that should not be confused, because they provide different opportunities for research.

Wednesday, July 4, 2018

I have already told you that with the help of which shamans try to sort ““ reality. How do they do this? How does the formation of a set actually occur?

Let's take a closer look at the definition of a set: "a collection of different elements, conceived as a single whole." Now feel the difference between two phrases: “conceivable as a whole” and “conceivable as a whole.” The first phrase is the end result, the set. The second phrase is a preliminary preparation for the formation of a multitude. At this stage, reality is divided into individual elements (the “whole”), from which a multitude will then be formed (the “single whole”). At the same time, the factor that makes it possible to combine the “whole” into a “single whole” is carefully monitored, otherwise the shamans will not succeed. After all, shamans know in advance exactly what set they want to show us.

I'll show you the process with an example. We select the “red solid in a pimple” - this is our “whole”. At the same time, we see that these things are with a bow, and there are without a bow. After that, we select part of the “whole” and form a set “with a bow”. This is how shamans get their food by tying their set theory to reality.

Now let's do a little trick. Let’s take “solid with a pimple with a bow” and combine these “wholes” according to color, selecting the red elements. We got a lot of "red". Now the final question: are the resulting sets “with a bow” and “red” the same set or two different sets? Only shamans know the answer. More precisely, they themselves do not know anything, but as they say, so it will be.

This simple example shows that set theory is completely useless when it comes to reality. What's the secret? We formed a set of "red solid with a pimple and a bow." The formation took place in four different units of measurement: color (red), strength (solid), roughness (pimply), decoration (with a bow). Only a set of units of measurement allows us to adequately describe real objects in the language of mathematics. This is what it looks like.

The letter "a" with different indices indicates different units of measurement. The units of measurement by which the “whole” is distinguished at the preliminary stage are highlighted in brackets. The unit of measurement by which the set is formed is taken out of brackets. The last line shows the final result - an element of the set. As you can see, if we use units of measurement to form a set, then the result does not depend on the order of our actions. And this is mathematics, and not the dancing of shamans with tambourines. Shamans can “intuitively” come to the same result, arguing that it is “obvious,” because units of measurement are not part of their “scientific” arsenal.

Using units of measurement it is very easy to break one
Today, everything that we do not take belongs to some set (as mathematicians assure us). By the way, did you see in the mirror on your forehead a list of those sets to which you belong? And I haven't seen such a list. I will say more - not a single thing in reality has a tag with a list of the sets to which this thing belongs. Sets are all inventions of shamans. How do they do it? Let's look a little deeper into history and see what the elements of the set looked like before the mathematician shamans took them into their sets.

A long time ago, when no one had ever heard of mathematics, and only trees and Saturn had rings, huge herds of wild elements of sets roamed the physical fields (after all, shamans had not yet invented mathematical fields). They looked something like this.

Yes, don’t be surprised, from the point of view of mathematics, all elements of sets are most similar to sea urchins - from one point, like needles, units of measurement stick out in all directions. For those who, I remind you that any unit of measurement can be geometrically represented as a segment of arbitrary length, and a number as a point. Geometrically, any quantity can be represented as a bunch of segments sticking out in different directions from one point. This point is point zero. I won’t draw this piece of geometric art (no inspiration), but you can easily imagine it.

What units of measurement form an element of a set? All sorts of things that describe a given element from different points of view. These are ancient units of measurement that our ancestors used and which everyone has long forgotten about. These are the modern units of measurement that we use now. These are also units of measurement unknown to us, which our descendants will come up with and which they will use to describe reality.

We've sorted out the geometry - the proposed model of the elements of the set has a clear geometric representation. What about physics? Units of measurement are the direct connection between mathematics and physics. If shamans do not recognize units of measurement as a full-fledged element of mathematical theories, this is their problem. I personally can’t imagine the real science of mathematics without units of measurement. That is why at the very beginning of the story about set theory I spoke of it as being in the Stone Age.

But let's move on to the most interesting thing - the algebra of elements of sets. Algebraically, any element of a set is a product (the result of multiplication) of different quantities. It looks like this.

I deliberately did not use the conventions of set theory, since we are considering an element of a set in its natural environment before the emergence of set theory. Each pair of letters in brackets denotes a separate quantity, consisting of a number indicated by the letter " n" and the unit of measurement indicated by the letter " a". The indices next to the letters indicate that the numbers and units of measurement are different. One element of the set can consist of an infinite number of quantities (how much we and our descendants have enough imagination). Each bracket is geometrically depicted as a separate segment. In the example with the sea urchin one bracket is one needle.

How do shamans form sets from different elements? In fact, by units of measurement or by numbers. Not understanding anything about mathematics, they take different sea urchins and carefully examine them in search of that single needle, along which they form a set. If there is such a needle, then this element belongs to the set; if there is no such needle, then this element is not from this set. Shamans tell us fables about thought processes and the whole.

As you may have guessed, the same element can belong to very different sets. Next I will show you how sets, subsets and other shamanic nonsense are formed.

When calculating examples, you need to follow a certain procedure. Using the rules below, we will figure out the order in which the actions are performed and what the parentheses are for.

If there are no parentheses in the expression, then:

first we perform all the operations of multiplication and division from left to right;

and then from left to right all the addition and subtraction operations.

Let's consider procedure in the following example.

We remind you that order of operations in mathematics arranged from left to right (from the beginning to the end of the example).

When calculating the value of an expression, you can record it in two ways.

First way

• Each action is recorded separately with its own number under the example.
• After the last action is completed, the response is necessarily written to the original example.



When calculating the results of actions with two-digit and/or three-digit numbers, be sure to list your calculations in a column.



Second way

• The second method is called chain recording. All calculations are carried out in exactly the same order, but the results are written immediately after the equal sign.

If the expression contains parentheses, then the actions in the parentheses are performed first.

Inside the parentheses themselves, the order of actions is the same as in expressions without parentheses.



If there are more brackets inside the brackets, then the actions inside the nested (inner) brackets are performed first.

Procedure and exponentiation

If the example contains a numeric or literal expression in brackets that must be raised to a power, then:

• First we perform all the actions inside the brackets
• Then we raise to a power all parentheses and numbers that stand in a power, from left to right (from the beginning to the end of the example).
• We carry out the remaining steps as usual



Procedure for performing actions, rules, examples.

Numeric, alphabetic expressions and expressions with variables in their notation may contain signs of various arithmetic operations. When transforming expressions and calculating the values ​​of expressions, actions are performed in a certain order, in other words, you must observe order of actions.

In this article, we will figure out which actions should be performed first and which ones after them. Let's start with the simplest cases, when the expression contains only numbers or variables connected by plus, minus, multiply and divide signs. Next, we will explain what order of actions should be followed in expressions with brackets. Finally, let's look at the order in which actions are performed in expressions containing powers, roots, and other functions.

Page navigation.

First multiplication and division, then addition and subtraction

The school gives the following a rule that determines the order in which actions are performed in expressions without parentheses:

• actions are performed in order from left to right,
• Moreover, multiplication and division are performed first, and then addition and subtraction.

The stated rule is perceived quite naturally. Performing actions in order from left to right is explained by the fact that it is customary for us to keep records from left to right. And the fact that multiplication and division are performed before addition and subtraction is explained by the meaning that these actions carry.

Let's look at a few examples of how this rule applies. For examples, we will take the simplest numerical expressions so as not to be distracted by calculations, but to focus specifically on the order of actions.

Follow steps 7−3+6.

The original expression does not contain parentheses, and it does not contain multiplication or division. Therefore, we should perform all actions in order from left to right, that is, first we subtract 3 from 7, we get 4, after which we add 6 to the resulting difference of 4, we get 10.

Briefly, the solution can be written as follows: 7−3+6=4+6=10.

Indicate the order of actions in the expression 6:2·8:3.

To answer the question of the problem, let's turn to the rule indicating the order of execution of actions in expressions without parentheses. The original expression contains only the operations of multiplication and division, and according to the rule, they must be performed in order from left to right.

First we divide 6 by 2, multiply this quotient by 8, and finally divide the result by 3.

Calculate the value of the expression 17−5·6:3−2+4:2.

First, let's determine in what order the actions in the original expression should be performed. It contains both multiplication and division and addition and subtraction. First, from left to right, you need to perform multiplication and division. So we multiply 5 by 6, we get 30, we divide this number by 3, we get 10. Now we divide 4 by 2, we get 2. We substitute the found value 10 into the original expression instead of 5·6:3, and instead of 4:2 - the value 2, we have 17−5·6:3−2+4:2=17−10−2+2.

The resulting expression no longer contains multiplication and division, so it remains to perform the remaining actions in order from left to right: 17−10−2+2=7−2+2=5+2=7 .

At first, in order not to confuse the order in which actions are performed when calculating the value of an expression, it is convenient to place numbers above the action signs that correspond to the order in which they are performed. For the previous example it would look like this: .

The same order of operations - first multiplication and division, then addition and subtraction - should be followed when working with letter expressions.

Actions of the first and second stages

In some mathematics textbooks there is a division of arithmetic operations into operations of the first and second stages. Let's figure this out.

Actions of the first stage addition and subtraction are called, and multiplication and division are called second stage actions.

In these terms, the rule from the previous paragraph, which determines the order of execution of actions, will be written as follows: if the expression does not contain parentheses, then in order from left to right, first the actions of the second stage (multiplication and division) are performed, then the actions of the first stage (addition and subtraction).

Order of arithmetic operations in expressions with parentheses

Expressions often contain parentheses to indicate the order in which actions are performed. In this case a rule that specifies the order of execution of actions in expressions with parentheses, is formulated as follows: first, the actions in brackets are performed, while multiplication and division are also performed in order from left to right, then addition and subtraction.

So, the expressions in brackets are considered as components of the original expression, and they retain the order of actions already known to us. Let's look at the solutions to the examples for greater clarity.

Follow these steps 5+(7−2·3)·(6−4):2.

The expression contains parentheses, so let's first perform the actions in the expressions enclosed in these parentheses. Let's start with the expression 7−2·3. In it you must first perform multiplication, and only then subtraction, we have 7−2·3=7−6=1. Let's move on to the second expression in brackets 6−4. There is only one action here - subtraction, we perform it 6−4 = 2.

We substitute the obtained values ​​into the original expression: 5+(7−2·3)·(6−4):2=5+1·2:2. In the resulting expression, we first perform multiplication and division from left to right, then subtraction, we get 5+1·2:2=5+2:2=5+1=6. At this point, all actions are completed, we adhered to the following order of their implementation: 5+(7−2·3)·(6−4):2.

Let's write down a short solution: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

It happens that an expression contains parentheses within parentheses. There is no need to be afraid of this; you just need to consistently apply the stated rule for performing actions in expressions with brackets. Let's show the solution of the example.

Perform the operations in the expression 4+(3+1+4·(2+3)) .

This is an expression with brackets, which means that the execution of actions must begin with the expression in brackets, that is, with 3+1+4·(2+3) . This expression also contains parentheses, so you must perform the actions in them first. Let's do this: 2+3=5. Substituting the found value, we get 3+1+4·5. In this expression, we first perform multiplication, then addition, we have 3+1+4·5=3+1+20=24. The initial value, after substituting this value, takes the form 4+24, and all that remains is to complete the actions: 4+24=28.

In general, when an expression contains parentheses within parentheses, it is often convenient to perform actions starting with the inner parentheses and moving to the outer ones.

For example, let's say we need to perform the actions in the expression (4+(4+(4−6:2))−1)−1. First, we perform the actions in the inner brackets, since 4−6:2=4−3=1, then after this the original expression will take the form (4+(4+1)−1)−1. We again perform the action in the inner brackets, since 4+1=5, we arrive at the following expression (4+5−1)−1. Again we perform the actions in brackets: 4+5−1=8, and we arrive at the difference 8−1, which is equal to 7.

The order of operations in expressions with roots, powers, logarithms and other functions

If the expression includes powers, roots, logarithms, sine, cosine, tangent and cotangent, as well as other functions, then their values ​​are calculated before performing other actions, and the rules from the previous paragraphs that specify the order of actions are also taken into account. In other words, the listed things, roughly speaking, can be considered enclosed in brackets, and we know that the actions in brackets are performed first.

Let's look at the solutions to the examples.

Perform the actions in the expression (3+1)·2+6 2:3−7.

This expression contains the power of 6 2, its value must be calculated before performing other actions. So, we perform the exponentiation: 6 2 =36. We substitute this value into the original expression, it will take the form (3+1)·2+36:3−7.

Then everything is clear: we perform the actions in brackets, after which we are left with an expression without brackets, in which, in order from left to right, we first perform multiplication and division, and then addition and subtraction. We have (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13.

You can see other, including more complex examples of performing actions in expressions with roots, powers, etc., in the article Calculating the Values ​​of Expressions.

cleverstudents.ru

Online games, simulators, presentations, lessons, encyclopedias, articles

Post navigation

Examples with brackets, lesson with simulators.

We will look at three examples in this article:

1. Examples with parentheses (addition and subtraction actions)

2. Examples with parentheses (addition, subtraction, multiplication, division)

3. Examples with a lot of action

1 Examples with parentheses (addition and subtraction operations)

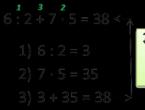
Let's look at three examples. In each of them, the order of actions is indicated by red numbers:



We see that the order of actions in each example will be different, although the numbers and signs are the same. This happens because there are parentheses in the second and third examples.

• If there are no parentheses in the example, we perform all actions in order, from left to right.
• If the example contains parentheses, then first we perform the actions in brackets, and only then all other actions, starting from left to right.

*This rule is for examples without multiplication and division. We will look at the rules for examples with parentheses involving the operations of multiplication and division in the second part of this article.

To avoid confusion in the example with parentheses, you can turn it into a regular example, without parentheses. To do this, write the result obtained in brackets above the brackets, then rewrite the entire example, writing this result instead of brackets, and then perform all the actions in order, from left to right:



In simple examples, you can perform all these operations in your mind. The main thing is to first perform the action in brackets and remember the result, and then count in order, from left to right.

And now - simulators!

1) Examples with brackets up to 20. Online simulator.



2) Examples with brackets up to 100. Online simulator.



3) Examples with brackets. Simulator No. 2



4) Insert the missing number - examples with brackets. Training apparatus



2 Examples with parentheses (addition, subtraction, multiplication, division)

Now let's look at examples in which, in addition to addition and subtraction, there is multiplication and division.

Let's look at examples without parentheses first:



• If there are no parentheses in the example, first perform the operations of multiplication and division in order, from left to right. Then - the operations of addition and subtraction in order, from left to right.
• If the example contains parentheses, then first we perform the operations in parentheses, then multiplication and division, and then addition and subtraction starting from left to right.

There is one trick to avoid getting confused when solving examples of the order of actions. If there are no parentheses, then we perform the operations of multiplication and division, then we rewrite the example, writing down the results obtained instead of these actions. Then we perform addition and subtraction in order:



If the example contains parentheses, then first you need to get rid of the parentheses: rewrite the example, writing the result obtained in them instead of the parentheses. Then you need to mentally highlight the parts of the example, separated by the signs “+” and “-“, and count each part separately. Then perform addition and subtraction in order:



3 Examples with a lot of action

If there are many actions in the example, then it will be more convenient not to arrange the order of actions in the entire example, but to select blocks and solve each block separately. To do this, we find free signs “+” and “–” (free means not in brackets, shown in the figure with arrows).

These signs will divide our example into blocks:

When performing actions in each block, do not forget about the procedure given above in the article. Having solved each block, we perform the addition and subtraction operations in order.

Now let’s consolidate the solution to the examples on the order of actions on the simulators!

1. Examples with parentheses within numbers up to 100, operations of addition, subtraction, multiplication and division. Online trainer.



2. Mathematics simulator for grades 2 - 3 “Arrange the order of actions (letter expressions).”



3. Order of actions (we arrange the order and solve examples)

Procedure in mathematics 4th grade

Primary school is coming to an end, and soon the child will step into the advanced world of mathematics. But already during this period the student is faced with the difficulties of science. When performing a simple task, the child gets confused and lost, which ultimately leads to a negative mark for the work done. To avoid such troubles, when solving examples, you need to be able to navigate in the order in which you need to solve the example. Having distributed the actions incorrectly, the child does not complete the task correctly. The article reveals the basic rules for solving examples that contain the entire range of mathematical calculations, including brackets. Procedure in mathematics 4th grade rules and examples.

Before completing the task, ask your child to number the actions that he is going to perform. If you have any difficulties, please help.

Some rules to follow when solving examples without brackets:

If a task requires a series of operations, you must first perform division or multiplication, then addition. All actions are performed as the letter progresses. Otherwise, the result of the decision will not be correct.

If in the example you need to perform addition and subtraction, we do it in order, from left to right.

27-5+15=37 (When solving the example, we are guided by the rule. First we perform subtraction, then addition).

Teach your child to always plan and number the actions performed.

The answers to each solved action are written above the example. This will make it much easier for the child to navigate the actions.

Let's consider another option where it is necessary to distribute actions in order:

As you can see, when solving, the rule is followed: first we look for the product, then we look for the difference.

These are simple examples that require careful consideration when solving them. Many children are stunned when they see a task that contains not only multiplication and division, but also parentheses. A student who does not know the procedure for performing actions has questions that prevent him from completing the task.

As stated in the rule, first we find the product or quotient, and then everything else. But there are parentheses! What to do in this case?

Solving examples with brackets

Let's look at a specific example:

• When performing this task, we first find the value of the expression enclosed in parentheses.
• You should start with multiplication, then addition.
• After the expression in brackets is solved, we proceed to actions outside them.
• According to the rules of procedure, the next step is multiplication.
• The final step will be subtraction.

As we can see in the visual example, all actions are numbered. To reinforce the topic, invite your child to solve several examples on their own:

The order in which the value of the expression should be calculated has already been arranged. The child will only have to carry out the decision directly.

Let's complicate the task. Let the child find the meaning of the expressions on his own.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Teach your child to solve all tasks in draft form. In this case, the student will have the opportunity to correct an incorrect decision or blots. Corrections are not allowed in the workbook. By completing tasks on their own, children see their mistakes.

Parents, in turn, should pay attention to mistakes, help the child understand and correct them. You shouldn’t overload a student’s brain with large amounts of tasks. With such actions you will discourage the child’s desire for knowledge. There should be a sense of proportion in everything.

Take a break. The child should be distracted and take a break from classes. The main thing to remember is that not everyone has a mathematical mind. Maybe your child will grow up to be a famous philosopher.

detskoerazvitie.info

Math lesson 2nd grade Order of actions in expressions with brackets.

Hurry up to take advantage of discounts of up to 50% on Infourok courses



Target: 1.

2.

3. Consolidate knowledge of the multiplication table and division by 2 – 6, the concept of divisor and

4. Learn to work in pairs in order to develop communication skills.

Equipment * : + — (), geometric material.

One, two - head up.

Three, four - arms wider.

Five, six - everyone sit down.

Seven, eight - let's discard laziness.

But first you have to find out its name. To do this you need to complete several tasks:

6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 dm 5 cm… 4 dm 5 cm

While we remembered the order of actions in expressions, miracles happened to the castle. We were just at the gate, and now we were in the corridor. Look, the door. And there is a castle on it. Shall we open it?

1. Subtract the quotient of 8 and 2 from the number 20.

2. Divide the difference between 20 and 8 by 2.

— How are the results different?

- Who can name the topic of our lesson?

(on massage mats)

Along the path, along the path

We gallop on our right leg,

We jump on our left leg.

Let's run along the path,

Our guess was completely correct7

Where are the actions performed first if there are parentheses in an expression?

Look at the “living examples” before us. Let's bring them to life.

* : + — ().

m – c * (a + d) + x

k: b + (a – c) * t

6. Work in pairs.

To solve them you will need geometric material.

Students complete tasks in pairs. After completion, check the work of the pairs at the board.

What new have you learned?

8. Homework.



Topic: Order of actions in expressions with brackets.

Target: 1. Derive a rule for the order of actions in expressions with brackets containing all

4 arithmetic operations,

2. To develop the ability to practically apply the rules,

4. Learn to work in pairs in order to develop communication skills.

Equipment: textbook, notebooks, cards with action signs * : + — (), geometric material.

1 .Physical exercise.

Nine, ten - sit down quietly.

2. Updating basic knowledge.

Today we are setting off on another journey through the Land of Knowledge, the city of mathematics. We have to visit one palace. Somehow I forgot its name. But let’s not be upset, you yourself can tell me its name. While I was worried, we approached the gates of the palace. Shall we come in?

1. Compare expressions:

2. Unscramble the word.

3. Statement of the problem. Discovery of something new.

So what is the name of the palace?

And when in mathematics do we talk about order?

What do you already know about the order of actions in expressions?

— Interesting, we are asked to write down and solve expressions (the teacher reads the expressions, the students write them down and solve them).

20 – 8: 2

(20 – 8) : 2

Well done. What's interesting about these expressions?

Look at the expressions and their results.

— What is common in writing expressions?

— Why do you think the results were different, since the numbers were the same?

Who would dare to formulate a rule for performing actions in expressions with brackets?

We can check the correctness of this answer in another room. Let's go there.

4. Physical exercise.

And along the same path

We will reach the mountain.

Stop. Let's rest a little

And we'll go on foot again.

5. Primary consolidation of what has been learned.

Here we are.

We need to solve two more expressions to check the correctness of our assumption.

6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2

To check the correctness of the assumption, let's open the textbooks on page 33 and read the rule.

How should you perform the actions after the solution in brackets?

Letter expressions are written on the board and there are cards with action signs. * : + — (). Children go to the board one at a time, take a card with the action that needs to be done first, then the second student comes out and takes a card with the second action, etc.

a + (a – b)

a * (b + c) : d – t

m – c * ( a + d ) + x

k : b + ( a – c ) * t

(a–b) : t+d

6. Work in pairs.

Knowing the order of actions is necessary not only for solving examples, but when solving problems we also encounter this rule. Now you will see this by working in pairs. You will need to solve problems from No. 3 p. 33.

• Features of accounting for subsidies The state seeks to support small and medium-sized businesses. Such support is most often expressed in the form of subsidies – free payments from […]
• Complaint against a pediatrician A complaint against a pediatrician is an official document establishing the patient’s requirements and describing the essence of such requirements. According to Article 4 of the Federal Law “On the Procedure for Consideration [...]
• Petition to reduce the size of the claim One of the types of clarification of the claim is a petition to reduce the size of the claim. When the plaintiff incorrectly determined the value of the claim. Or the defendant partially fulfilled [...]
• Black market for dollars in Kyiv Currency auction for buying dollars in Kyiv Attention: the administration is not responsible for the content of advertisements at the currency auction. Rules for publishing advertisements on foreign exchange […]

And when calculating the values ​​of expressions, actions are performed in a certain order, in other words, you must observe order of actions.

In this article, we will figure out which actions should be performed first and which ones after them. Let's start with the simplest cases, when the expression contains only numbers or variables connected by plus, minus, multiply and divide signs. Next, we will explain what order of actions should be followed in expressions with brackets. Finally, let's look at the order in which actions are performed in expressions containing powers, roots, and other functions.

Page navigation.

First multiplication and division, then addition and subtraction

The school gives the following a rule that determines the order in which actions are performed in expressions without parentheses:

• actions are performed in order from left to right,
• Moreover, multiplication and division are performed first, and then addition and subtraction.

The stated rule is perceived quite naturally. Performing actions in order from left to right is explained by the fact that it is customary for us to keep records from left to right. And the fact that multiplication and division are performed before addition and subtraction is explained by the meaning that these actions carry.

Let's look at a few examples of how this rule applies. For examples, we will take the simplest numerical expressions so as not to be distracted by calculations, but to focus specifically on the order of actions.

Example.

Follow steps 7−3+6.

Solution.

The original expression does not contain parentheses, and it does not contain multiplication or division. Therefore, we should perform all actions in order from left to right, that is, first we subtract 3 from 7, we get 4, after which we add 6 to the resulting difference of 4, we get 10.

Briefly, the solution can be written as follows: 7−3+6=4+6=10.

Answer:

7−3+6=10 .

Example.

Indicate the order of actions in the expression 6:2·8:3.

Solution.

To answer the question of the problem, let's turn to the rule indicating the order of execution of actions in expressions without parentheses. The original expression contains only the operations of multiplication and division, and according to the rule, they must be performed in order from left to right.

Answer:

At first We divide 6 by 2, multiply this quotient by 8, and finally divide the result by 3.

Example.

Calculate the value of the expression 17−5·6:3−2+4:2.

Solution.

First, let's determine in what order the actions in the original expression should be performed. It contains both multiplication and division and addition and subtraction. First, from left to right, you need to perform multiplication and division. So we multiply 5 by 6, we get 30, we divide this number by 3, we get 10. Now we divide 4 by 2, we get 2. We substitute the found value 10 into the original expression instead of 5·6:3, and instead of 4:2 - the value 2, we have 17−5·6:3−2+4:2=17−10−2+2.

The resulting expression no longer contains multiplication and division, so it remains to perform the remaining actions in order from left to right: 17−10−2+2=7−2+2=5+2=7 .

Answer:

17−5·6:3−2+4:2=7.

At first, in order not to confuse the order in which actions are performed when calculating the value of an expression, it is convenient to place numbers above the action signs that correspond to the order in which they are performed. For the previous example it would look like this: .

The same order of operations - first multiplication and division, then addition and subtraction - should be followed when working with letter expressions.

Actions of the first and second stages

In some mathematics textbooks there is a division of arithmetic operations into operations of the first and second stages. Let's figure this out.

Definition.

Actions of the first stage addition and subtraction are called, and multiplication and division are called second stage actions.

In these terms, the rule from the previous paragraph, which determines the order of execution of actions, will be written as follows: if the expression does not contain parentheses, then in order from left to right, first the actions of the second stage (multiplication and division) are performed, then the actions of the first stage (addition and subtraction).

Order of arithmetic operations in expressions with parentheses

Expressions often contain parentheses to indicate the order in which actions should be performed. In this case a rule that specifies the order of execution of actions in expressions with parentheses, is formulated as follows: first, the actions in brackets are performed, while multiplication and division are also performed in order from left to right, then addition and subtraction.

So, the expressions in brackets are considered as components of the original expression, and they retain the order of actions already known to us. Let's look at the solutions to the examples for greater clarity.

Example.

Follow these steps 5+(7−2·3)·(6−4):2.

Solution.

The expression contains parentheses, so let's first perform the actions in the expressions enclosed in these parentheses. Let's start with the expression 7−2·3. In it you must first perform multiplication, and only then subtraction, we have 7−2·3=7−6=1. Let's move on to the second expression in brackets 6−4. There is only one action here - subtraction, we perform it 6−4 = 2.

We substitute the obtained values ​​into the original expression: 5+(7−2·3)·(6−4):2=5+1·2:2. In the resulting expression, we first perform multiplication and division from left to right, then subtraction, we get 5+1·2:2=5+2:2=5+1=6. At this point, all actions are completed, we adhered to the following order of their implementation: 5+(7−2·3)·(6−4):2.

Let's write down a short solution: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

Answer:

5+(7−2·3)·(6−4):2=6.

It happens that an expression contains parentheses within parentheses. There is no need to be afraid of this; you just need to consistently apply the stated rule for performing actions in expressions with brackets. Let's show the solution of the example.

Example.

Perform the operations in the expression 4+(3+1+4·(2+3)) .

Solution.

This is an expression with brackets, which means that the execution of actions must begin with the expression in brackets, that is, with 3+1+4·(2+3) . This expression also contains parentheses, so you must perform the actions in them first. Let's do this: 2+3=5. Substituting the found value, we get 3+1+4·5. In this expression, we first perform multiplication, then addition, we have 3+1+4·5=3+1+20=24. The initial value, after substituting this value, takes the form 4+24, and all that remains is to complete the actions: 4+24=28.

Answer:

4+(3+1+4·(2+3))=28.

In general, when an expression contains parentheses within parentheses, it is often convenient to perform actions starting with the inner parentheses and moving to the outer ones.

For example, let's say we need to perform the actions in the expression (4+(4+(4−6:2))−1)−1. First, we perform the actions in the inner brackets, since 4−6:2=4−3=1, then after this the original expression will take the form (4+(4+1)−1)−1. We again perform the action in the inner brackets, since 4+1=5, we arrive at the following expression (4+5−1)−1. Again we perform the actions in brackets: 4+5−1=8, and we arrive at the difference 8−1, which is equal to 7.

The original source is located. Alpha stands for real number. The equal sign in the above expressions indicates that if you add a number or infinity to infinity, nothing will change, the result will be the same infinity. If we take the infinite set of natural numbers as an example, then the considered examples can be represented in this form:

To clearly prove that they were right, mathematicians came up with many different methods. Personally, I look at all these methods as shamans dancing with tambourines. Essentially, they all boil down to the fact that either some of the rooms are unoccupied and new guests are moving in, or that some of the visitors are thrown out into the corridor to make room for guests (very humanly). I presented my view on such decisions in the form of a fantasy story about the Blonde. What is my reasoning based on? Relocating an infinite number of visitors takes an infinite amount of time. After we have vacated the first room for a guest, one of the visitors will always walk along the corridor from his room to the next one until the end of time. Of course, the time factor can be stupidly ignored, but this will be in the category of “no law is written for fools.” It all depends on what we are doing: adjusting reality to mathematical theories or vice versa.

What is an “endless hotel”? An infinite hotel is a hotel that always has any number of empty beds, regardless of how many rooms are occupied. If all the rooms in the endless "visitor" corridor are occupied, there is another endless corridor with "guest" rooms. There will be an infinite number of such corridors. Moreover, the “infinite hotel” has an infinite number of floors in an infinite number of buildings on an infinite number of planets in an infinite number of universes created by an infinite number of Gods. Mathematicians are not able to distance themselves from banal everyday problems: there is always only one God-Allah-Buddha, there is only one hotel, there is only one corridor. So mathematicians are trying to juggle the serial numbers of hotel rooms, convincing us that it is possible to “shove in the impossible.”

I will demonstrate the logic of my reasoning to you using the example of an infinite set of natural numbers. First you need to answer a very simple question: how many sets of natural numbers are there - one or many? There is no correct answer to this question, since we invented numbers ourselves; numbers do not exist in Nature. Yes, Nature is great at counting, but for this she uses other mathematical tools that are not familiar to us. I’ll tell you what Nature thinks another time. Since we invented numbers, we ourselves will decide how many sets of natural numbers there are. Let's consider both options, as befits real scientists.

Option one. “Let us be given” one single set of natural numbers, which lies serenely on the shelf. We take this set from the shelf. That's it, there are no other natural numbers left on the shelf and nowhere to take them. We cannot add one to this set, since we already have it. What if you really want to? No problem. We can take one from the set we have already taken and return it to the shelf. After that, we can take one from the shelf and add it to what we have left. As a result, we will again get an infinite set of natural numbers. You can write down all our manipulations like this:

I wrote down the actions in algebraic notation and in set theory notation, with a detailed listing of the elements of the set. The subscript indicates that we have one and only set of natural numbers. It turns out that the set of natural numbers will remain unchanged only if one is subtracted from it and the same unit is added.

Option two. We have many different infinite sets of natural numbers on our shelf. I emphasize - DIFFERENT, despite the fact that they are practically indistinguishable. Let's take one of these sets. Then we take one from another set of natural numbers and add it to the set we have already taken. We can even add two sets of natural numbers. This is what we get:

The subscripts "one" and "two" indicate that these elements belonged to different sets. Yes, if you add one to an infinite set, the result will also be an infinite set, but it will not be the same as the original set. If you add another infinite set to one infinite set, the result is a new infinite set consisting of the elements of the first two sets.

The set of natural numbers is used for counting in the same way as a ruler is for measuring. Now imagine that you added one centimeter to the ruler. This will be a different line, not equal to the original one.

You can accept or not accept my reasoning - it is your own business. But if you ever encounter mathematical problems, think about whether you are following the path of false reasoning trodden by generations of mathematicians. After all, studying mathematics, first of all, forms a stable stereotype of thinking in us, and only then adds to our mental abilities (or, conversely, deprives us of free-thinking).

pozg.ru

Sunday, August 4, 2019

I was finishing a postscript to an article about and saw this wonderful text on Wikipedia:

We read: "... the rich theoretical basis of the mathematics of Babylon did not have a holistic character and was reduced to a set of disparate techniques, devoid of a common system and evidence base."

Wow! How smart we are and how well we can see the shortcomings of others. Is it difficult for us to look at modern mathematics in the same context? Slightly paraphrasing the above text, I personally got the following:

The rich theoretical basis of modern mathematics is not holistic in nature and is reduced to a set of disparate sections, devoid of a common system and evidence base.

I won’t go far to confirm my words - it has a language and conventions that are different from the language and conventions of many other branches of mathematics. The same names in different branches of mathematics can have different meanings. I want to devote a whole series of publications to the most obvious mistakes of modern mathematics. See you soon.

Saturday, August 3, 2019

How to divide a set into subsets? To do this, you need to enter a new unit of measurement that is present in some of the elements of the selected set. Let's look at an example.

May we have plenty A consisting of four people. This set is formed on the basis of “people.” Let us denote the elements of this set by the letter A, the subscript with a number will indicate the serial number of each person in this set. Let's introduce a new unit of measurement "gender" and denote it by the letter b. Since sexual characteristics are inherent in all people, we multiply each element of the set A based on gender b. Notice that our set of “people” has now become a set of “people with gender characteristics.” After this we can divide the sexual characteristics into male bm and women's bw sexual characteristics. Now we can apply a mathematical filter: we select one of these sexual characteristics, no matter which one - male or female. If a person has it, then we multiply it by one, if there is no such sign, we multiply it by zero. And then we use regular school mathematics. Look what happened.

After multiplication, reduction and rearrangement, we ended up with two subsets: the subset of men Bm and a subset of women Bw. Mathematicians reason in approximately the same way when they apply set theory in practice. But they don’t tell us the details, but give us the finished result - “a lot of people consist of a subset of men and a subset of women.” Naturally, you may have a question: how correctly has the mathematics been applied in the transformations outlined above? I dare to assure you that essentially everything was done correctly; it is enough to know the mathematical basis of arithmetic, Boolean algebra and other branches of mathematics. What it is? Some other time I will tell you about this.

As for supersets, you can combine two sets into one superset by selecting the unit of measurement present in the elements of these two sets.

As you can see, units of measurement and ordinary mathematics make set theory a relic of the past. A sign that all is not well with set theory is that mathematicians have come up with their own language and notation for set theory. Mathematicians acted as shamans once did. Only shamans know how to “correctly” apply their “knowledge.” They teach us this “knowledge”.

In conclusion, I want to show you how mathematicians manipulate .

Monday, January 7, 2019

In the fifth century BC, the ancient Greek philosopher Zeno of Elea formulated his famous aporias, the most famous of which is the “Achilles and the Tortoise” aporia. Here's what it sounds like:

Let's say Achilles runs ten times faster than the tortoise and is a thousand steps behind it. During the time it takes Achilles to run this distance, the tortoise will crawl a hundred steps in the same direction. When Achilles runs a hundred steps, the tortoise crawls another ten steps, and so on. The process will continue ad infinitum, Achilles will never catch up with the tortoise.

This reasoning became a logical shock for all subsequent generations. Aristotle, Diogenes, Kant, Hegel, Hilbert... They all considered Zeno's aporia in one way or another. The shock was so strong that " ... discussions continue to this day; the scientific community has not yet been able to come to a common opinion on the essence of paradoxes ... mathematical analysis, set theory, new physical and philosophical approaches were involved in the study of the issue; none of them became a generally accepted solution to the problem..."[Wikipedia, "Zeno's Aporia". Everyone understands that they are being fooled, but no one understands what the deception consists of.

From a mathematical point of view, Zeno in his aporia clearly demonstrated the transition from quantity to . This transition implies application instead of permanent ones. As far as I understand, the mathematical apparatus for using variable units of measurement has either not yet been developed, or it has not been applied to Zeno’s aporia. Applying our usual logic leads us into a trap. We, due to the inertia of thinking, apply constant units of time to the reciprocal value. From a physical point of view, this looks like time slowing down until it stops completely at the moment when Achilles catches up with the turtle. If time stops, Achilles can no longer outrun the tortoise.

If we turn our usual logic around, everything falls into place. Achilles runs at a constant speed. Each subsequent segment of his path is ten times shorter than the previous one. Accordingly, the time spent on overcoming it is ten times less than the previous one. If we apply the concept of “infinity” in this situation, then it would be correct to say “Achilles will catch up with the turtle infinitely quickly.”

How to avoid this logical trap? Remain in constant units of time and do not switch to reciprocal units. In Zeno's language it looks like this:

In the time it takes Achilles to run a thousand steps, the tortoise will crawl a hundred steps in the same direction. During the next time interval equal to the first, Achilles will run another thousand steps, and the tortoise will crawl a hundred steps. Now Achilles is eight hundred steps ahead of the tortoise.

This approach adequately describes reality without any logical paradoxes. But this is not a complete solution to the problem. Einstein’s statement about the irresistibility of the speed of light is very similar to Zeno’s aporia “Achilles and the Tortoise”. We still have to study, rethink and solve this problem. And the solution must be sought not in infinitely large numbers, but in units of measurement.

Another interesting aporia of Zeno tells about a flying arrow:

A flying arrow is motionless, since at every moment of time it is at rest, and since it is at rest at every moment of time, it is always at rest.

In this aporia, the logical paradox is overcome very simply - it is enough to clarify that at each moment of time a flying arrow is at rest at different points in space, which, in fact, is motion. Another point needs to be noted here. From one photograph of a car on the road it is impossible to determine either the fact of its movement or the distance to it. To determine whether a car is moving, you need two photographs taken from the same point at different points in time, but you cannot determine the distance from them. To determine the distance to a car, you need two photographs taken from different points in space at one point in time, but from them you cannot determine the fact of movement (of course, you still need additional data for calculations, trigonometry will help you). What I want to draw special attention to is that two points in time and two points in space are different things that should not be confused, because they provide different opportunities for research.

Wednesday, July 4, 2018

I have already told you that with the help of which shamans try to sort ““ reality. How do they do this? How does the formation of a set actually occur?

Let's take a closer look at the definition of a set: "a collection of different elements, conceived as a single whole." Now feel the difference between two phrases: “conceivable as a whole” and “conceivable as a whole.” The first phrase is the end result, the set. The second phrase is a preliminary preparation for the formation of a multitude. At this stage, reality is divided into individual elements (the “whole”), from which a multitude will then be formed (the “single whole”). At the same time, the factor that makes it possible to combine the “whole” into a “single whole” is carefully monitored, otherwise the shamans will not succeed. After all, shamans know in advance exactly what set they want to show us.

I'll show you the process with an example. We select the “red solid in a pimple” - this is our “whole”. At the same time, we see that these things are with a bow, and there are without a bow. After that, we select part of the “whole” and form a set “with a bow”. This is how shamans get their food by tying their set theory to reality.

Now let's do a little trick. Let’s take “solid with a pimple with a bow” and combine these “wholes” according to color, selecting the red elements. We got a lot of "red". Now the final question: are the resulting sets “with a bow” and “red” the same set or two different sets? Only shamans know the answer. More precisely, they themselves do not know anything, but as they say, so it will be.

This simple example shows that set theory is completely useless when it comes to reality. What's the secret? We formed a set of "red solid with a pimple and a bow." The formation took place in four different units of measurement: color (red), strength (solid), roughness (pimply), decoration (with a bow). Only a set of units of measurement allows us to adequately describe real objects in the language of mathematics. This is what it looks like.

The letter "a" with different indices indicates different units of measurement. The units of measurement by which the “whole” is distinguished at the preliminary stage are highlighted in brackets. The unit of measurement by which the set is formed is taken out of brackets. The last line shows the final result - an element of the set. As you can see, if we use units of measurement to form a set, then the result does not depend on the order of our actions. And this is mathematics, and not the dancing of shamans with tambourines. Shamans can “intuitively” come to the same result, arguing that it is “obvious,” because units of measurement are not part of their “scientific” arsenal.

Using units of measurement it is very easy to break one
Today, everything that we do not take belongs to some set (as mathematicians assure us). By the way, did you see in the mirror on your forehead a list of those sets to which you belong? And I haven't seen such a list. I will say more - not a single thing in reality has a tag with a list of the sets to which this thing belongs. Sets are all inventions of shamans. How do they do it? Let's look a little deeper into history and see what the elements of the set looked like before the mathematician shamans took them into their sets.

A long time ago, when no one had ever heard of mathematics, and only trees and Saturn had rings, huge herds of wild elements of sets roamed the physical fields (after all, shamans had not yet invented mathematical fields). They looked something like this.

Yes, don’t be surprised, from the point of view of mathematics, all elements of sets are most similar to sea urchins - from one point, like needles, units of measurement stick out in all directions. For those who, I remind you that any unit of measurement can be geometrically represented as a segment of arbitrary length, and a number as a point. Geometrically, any quantity can be represented as a bunch of segments sticking out in different directions from one point. This point is point zero. I won’t draw this piece of geometric art (no inspiration), but you can easily imagine it.

What units of measurement form an element of a set? All sorts of things that describe a given element from different points of view. These are ancient units of measurement that our ancestors used and which everyone has long forgotten about. These are the modern units of measurement that we use now. These are also units of measurement unknown to us, which our descendants will come up with and which they will use to describe reality.

We've sorted out the geometry - the proposed model of the elements of the set has a clear geometric representation. What about physics? Units of measurement are the direct connection between mathematics and physics. If shamans do not recognize units of measurement as a full-fledged element of mathematical theories, this is their problem. I personally can’t imagine the real science of mathematics without units of measurement. That is why at the very beginning of the story about set theory I spoke of it as being in the Stone Age.

But let's move on to the most interesting thing - the algebra of elements of sets. Algebraically, any element of a set is a product (the result of multiplication) of different quantities. It looks like this.

I deliberately did not use the conventions of set theory, since we are considering an element of a set in its natural environment before the emergence of set theory. Each pair of letters in brackets denotes a separate quantity, consisting of a number indicated by the letter " n" and the unit of measurement indicated by the letter " a". The indices next to the letters indicate that the numbers and units of measurement are different. One element of the set can consist of an infinite number of quantities (how much we and our descendants have enough imagination). Each bracket is geometrically depicted as a separate segment. In the example with the sea urchin one bracket is one needle.

How do shamans form sets from different elements? In fact, by units of measurement or by numbers. Not understanding anything about mathematics, they take different sea urchins and carefully examine them in search of that single needle, along which they form a set. If there is such a needle, then this element belongs to the set; if there is no such needle, then this element is not from this set. Shamans tell us fables about thought processes and the whole.

As you may have guessed, the same element can belong to very different sets. Next I will show you how sets, subsets and other shamanic nonsense are formed.