A harmadik bizonyítással párhuzamos két egyenes tulajdonsága. Két egyenes vonal párhuzamosságának jelei. A párhuzamos vonalak tulajdonságai. Vonalak párhuzamossága - a párhuzamosság jelei és feltételei

Két egyenes párhuzamossága a tétel alapján bizonyítható, miszerint két egyenesre vetített merőleges párhuzamos lesz. Az egyenes vonalak párhuzamosságának bizonyos jelei vannak - hárman vannak, és ezeket mind konkrétabban megvizsgáljuk.

A párhuzamosság első jele

A vonalak párhuzamosak, ha harmadik vonaluk metszéspontjában a kialakult belső keresztirányú szögek egyenlőek lesznek.

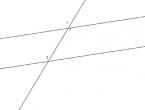
Tegyük fel, hogy az AB és CD egyenesek EF egyenes metszéspontjában az / 1 és / 2 szögek képződtek. Egyenlőek, mivel az EF egyenes egy lejtőn fut a másik két egyeneshez képest. A vonalak metszéspontjában a Ki L pontokat tesszük - megkapjuk a szekundáns EF metszetét. Megtaláljuk a közepét, és betesszük az O pontot (189. ábra).

Az AB vonalon elengedjük a merőlegest az O pontról. Nevezzük OM-nek. Addig folytatjuk a merőlegest, amíg az keresztezi a CD egyenes vonalát. Ennek eredményeként az eredeti AB egyenes merőleges az МN-re, ami azt jelenti, hogy СD_ | _МN, de ez az állítás bizonyítást igényel. A merőleges és a metszésvonal megrajzolásának eredményeként két háromszöget alakítottunk ki. Az egyik MOE, a második NOK. Vizsgáljuk meg őket részletesebben. az egyenesek párhuzamosságának jelei 7 fokozatú

Ezek a háromszögek egyenlők, mivel a tétel feltételeinek megfelelően / 1 \u003d / 2 és a háromszögek felépítésével összhangban az ОK \u003d az oldal ОL. MOL \u003d / NOK szög, mivel ezek függőleges szögek. Ebből következik, hogy az egyik háromszög oldala és a vele szomszédos két szög egyenlő a másik háromszög oldalával és a vele szomszédos két szöggel. Így a MOL \u003d NOK háromszög, tehát az LMO \u003d KNO szög, de tudjuk, hogy az / LMO egyenes, ami azt jelenti, hogy a megfelelő KNO szög is igaz. Vagyis sikerült bizonyítani, hogy a МN egyenesre mind az AB, mind a CD egyenes merőleges. Vagyis az AB és a CD párhuzamosak egymással. Ezt kellett bizonyítanunk. Vegyük figyelembe az egyenes vonalak párhuzamosságának fennmaradó kritériumait (7. fokozat), amelyek a bizonyítás tekintetében különböznek az első kritériumtól.

A párhuzamosság második jele

Az egyenesek párhuzamosságának második kritériuma szerint be kell bizonyítanunk, hogy az EF egyenes AB és CD párhuzamos egyenesének metszésében kapott szögek megegyeznek. Így két egyenes, az első és a második párhuzamosságának jelei a harmadik vonallal való metszéskor kapott szögek egyenlőségén alapulnak. Feltételezzük, hogy / 3 \u003d / 2, és az 1 \u003d / 3 szög, mivel függőleges hozzá. Így az u / 2 egyenlő lesz az 1. szöggel, de nem szabad megfeledkezni arról, hogy az 1. és a 2. szög egyaránt belső, keresztben fekvő szög. Ezért továbbra is alkalmaznunk kell tudásunkat, nevezetesen azt, hogy két szegmens párhuzamos lesz, ha a harmadik egyenes metszéspontjában a keresztben kialakult szögek megegyeznek. Így megtudtuk, hogy az AB || CD.

Bizonyítani tudtuk, hogy feltéve, hogy két merőleges párhuzamosan áll egy egyenesre, a megfelelő tétel szerint a párhuzamos vonalak kritériuma nyilvánvaló.

A párhuzamosság harmadik jele

Van egy harmadik párhuzamossági jel is, amelyet az egyoldalú belső szögek összege bizonyít. Az egyenesek párhuzamosságának kritériumának ilyen bizonyítása lehetővé teszi azt a következtetést, hogy két egyenes párhuzamos lesz, ha a harmadik egyenesük metszésénél a kapott egyoldalas belső szögek összege megegyezik 2d-vel. Lásd a 192. ábrát.

A párhuzamosság nagyon hasznos tulajdonság a geometriában. A való életben a párhuzamos oldalak lehetővé teszik gyönyörű, szimmetrikus dolgok létrehozását, amelyek tetszetősek minden szem számára, ezért a geometriának mindig is szüksége volt ennek a párhuzamosságnak a ellenőrzésére. Ebben a cikkben a párhuzamos vonalak jeleiről fogunk beszélni.

A párhuzamosság meghatározása

Emeljük ki azokat a definíciókat, amelyeket ismerni kell a két vonal párhuzamosságának kritériumai bizonyításához.

A vonalakat párhuzamosnak nevezzük, ha nincs metszéspontjuk. Ezenkívül a megoldásokban a párhuzamos egyenesek általában egy szekunder vonallal együtt mennek.

A vágási vonal egyenes, amely metszi mindkét párhuzamos vonalat. Ebben az esetben keresztben fekvő, ennek megfelelő és egyoldalú szögek képződnek. Az 1. és 4. szög párjai keresztben fekszenek; 2. és 3.; 8. és 6.; A megfelelő 7 és 2 lesz; 1. és 6.; 8. és 4.; 3. és 5. ábra.

Egyoldalú 1 és 2; 7. és 6.; 8. és 5.; 3. és 4. ábra.

A helyes kialakítással ez van írva: "Keresztirányban fekvő szögek két párhuzamos a és b egyenesre és c szekunderre", mert két párhuzamos vonalnál végtelen számú szekundum létezhet, ezért meg kell jelölni, hogy melyik szekánsra gondolsz.

Ezenkívül a bizonyításhoz szükség van a háromszög külső szögére vonatkozó tételre, amely azt mondja, hogy a háromszög külső szöge megegyezik egy háromszög két szögének összegével, amelyek nem szomszédosak vele.

Jelek

A párhuzamos vonalak minden előjele a szögek és a háromszög külső szögén található tétel ismeretéhez kapcsolódik.

1. jellemző

Két egyenes párhuzamos, ha a keresztben fekvő szögek egyenlőek.

Vegyünk két egyenes vonalat a és b szekundánssal. Az 1. és 4. keresztirányú fekvésszög egyenlő. Tegyük fel, hogy a vonalak nem párhuzamosak. Tehát az egyenesek keresztezik egymást, és legyen egy M. metszéspont. Ezután egy ABM háromszög képződik, amelynek külső szöge 1. A külső szögnek meg kell egyeznie a 4 és az ABM szögek összegével, mivel nem szomszédosak vele a háromszögben lévő külső szögre vonatkozó tétel szerint. De ekkor kiderül, hogy az 1 szög nagyobb, mint a 4 szög, és ez ellentmond a probléma feltételének, ami azt jelenti, hogy az M pont nem létezik, a vonalak nem keresztezik egymást, vagyis párhuzamosak.

Ábra: 1. Rajz a bizonyításhoz.

2. jel

Két egyenes párhuzamos, ha a megfelelő szög a szekundán egyenlő.

Tekintsünk két a és b egyeneset a c szekundánssal. A megfelelő 7 és 2 szög egyenlő. Jegyezze meg a 3. szöget. A 7. szög függőleges. Tehát a 7. és 3. szög egyenlő. Ezért a 3. és 2. szög is egyenlő, mivel<7=<2 и <7=<3. А угол 3 и угол 2 являются накрест лежащими. Следовательно, прямые параллельны, что и требовалось доказать.

Ábra: 2. Rajz a bizonyításhoz.

3. jellemző

Két egyenes párhuzamos, ha az egyoldalas szögek összege 180 fok.

Ábra: 3. Rajz a bizonyításhoz.

Tekintsünk két a és b egyeneset a c szekundánssal. Az 1. és 2. oldalszög 180 fokot tesz ki. Ügyeljen az 1. és a 7. szögre. Ezek szomszédosak. Azaz:

$$<1+<7=180$$

$$<1+<2=180$$

Vonja le a másodikat az első kifejezésből:

$$(<1+<7)-(<1+<2)=180-180$$

$$(<1+<7)-(<1+<2)=0$$

$$<1+<7-<1-<2=0$$

$$<7-<2=0$$

$<7=<2$ - а они являются соответственными. Значит, прямые параллельны.

Mit tanultunk?

Részletesen elemeztük, hogy milyen szögeket kapunk a párhuzamos egyenesek harmadik vonallal történő elvágásával, azonosítottuk és részletesen leírtuk a párhuzamos vonalak három előjelének bizonyítását.

Téma szerint tesztelni

Cikk értékelése

Átlagos értékelés: 4.1. Összes kapott értékelés: 220.

1. meghatározás

A $ -ot a $ -val meghívjuk metsző a $ a $ és $ b $ egyenesek esetén, ha két pontban metszik őket.

Tekintsünk két $ a $ és $ b $ sort, valamint egy $ másodlagos sort $ -val.

Amikor keresztezik egymást, szögek keletkeznek, amelyeket $ 1 $ és $ 8 $ közötti számokkal jelölünk.

Ezen szögek mindegyikének van egy neve, amelyet gyakran használnak a matematikában:

pár sarok $ 3 $ és $ 5 $, $ 4 $ és $ 6 $ hívják meg keresztben fekve;
pár sarok $ 1 $ és $ 5 $, $ 4 $ és $ 8 $, $ 2 $ és $ 6 $, $ 3 $ és $ 7 $ a megfelelő;
$ 4 $ és $ 5 $, $ 5 $ és $ 6 $ szögpárokat hívnak meg egyoldalú.

Az egyenes vonalak párhuzamosságának jelei

1. tétel

A kereszteződő szögpár egyenlősége a $ a $ és $ b $ egyeneseknél, valamint a szekunder $ c $ azt jelzi, hogy a $ a $ és $ b $ egyenesek párhuzamosak:

Bizonyíték.

Legyen egyenlő a $ a $ és $ b $ egyenesek és a szekunder $ c $ metsző szöge: $ ∠1 \u003d ∠2 $.

Mutassuk meg, hogy $ a \\ párhuzamos b $.

Feltéve, hogy a $ 1 $ és a $ 2 $ szögek egyenesek, megkapjuk, hogy a $ a $ és $ b $ egyenesek merőlegesek az $ AB $ egyenesre, és ezért párhuzamosak.

Feltéve, hogy a $ 1 $ és a $ 2 $ szögek nem egyenesek, húzzunk az $ O $ ponttól - a $ AB $ szakasz közepétől, merőlegesen a $ OH $ -ra a $ a $ egyenesre.

A $ b $ egyenesen elhalasztjuk a $ BH_1 \u003d AH $ szakaszt, és felhívjuk a $ OH_1 $ szakaszt. Két egyenlő háromszöget kapunk $ ОНА $ és $ ОH_1В $ két oldal mentén és egy szöget közöttük ($ ∠1 \u003d ∠2 $, $ AO \u003d BO $, $ BH_1 \u003d AH $), ezért $ ∠3 \u003d ∠4 $ és $ ∠5 \u003d ∠6 $. Mivel $ ∠3 \u003d ∠4 $, akkor a $ H_1 $ pont a $ ОН $ sugáron fekszik, így a $ Н $, $ О $ és $ H_1 $ pontok egy egyeneshez tartoznak. Mivel $ ∠5 \u003d ∠6 $, majd $ ∠6 \u003d 90 ^ (\\ circ) $. Így a $ a $ és $ b $ egyenesek merőlegesek a $ HH_1 $ egyenesre párhuzamosak. A tétel bebizonyosodott.

2. tétel

A $ a $ és $ b $ egyenesek megfelelő szögpárjának és a szekunder $ c $ egyenlősége azt jelzi, hogy az $ a $ és $ b $ egyenesek párhuzamosak:

ha $ ∠1 \u003d ∠2 $, akkor $ a \\ párhuzamos b $.

Bizonyíték.

Legyen egyenlő a $ a $ és $ b $ egyenesek és a szekunder $ c $ megfelelő szöge: $ ∠1 \u003d ∠2 $. A $ 2 $ és a $ 3 $ sarkok függőlegesek, tehát $ ∠2 \u003d ∠3 $. Ezért $ ∠1 \u003d ∠3 $. Mivel a $ 1 $ és a $ 3 $ szögek keresztben vannak, akkor a $ a $ és $ b $ vonalak párhuzamosak. A tétel bebizonyosodott.

3. tétel

Ha a $ a $ és $ b $ egyenesek és a szekunder $ c $ két egyoldalas szögének összege megegyezik $ 180 ^ (\\ circ) C $ értékkel, akkor a $ a $ és $ b $ egyenesek párhuzamosak:

ha $ ∠1 + ∠4 \u003d 180 ^ (\\ circ) $, akkor $ a \\ párhuzamos b $.

Bizonyíték.

Hagyja, hogy az $ a $ és $ b $ vonalak és a szekunder $ c $ egyoldalú szöge például $ 180 ^ (\\ circ) $ legyen.

$ ∠1 + ∠4 \u003d 180 ^ (\\ circ) $.

A $ 3 $ és a $ 4 $ sarkok szomszédosak, tehát

$ ∠3 + ∠4 \u003d 180 ^ (\\ circ) $.

A kapott egyenlőségekből látható, hogy a kereszteződő $ ∠1 \u003d ∠3 $ szögek, ebből következik, hogy a $ a $ és $ b $ egyenesek párhuzamosak.

A tétel bebizonyosodott.

A figyelembe vett jellemzőkből következik az egyenes vonalak párhuzamossága.

Példák a problémamegoldásra

1. példa

A kereszteződés felezi az $ AB $ és a $ CD $ szakaszokat. Bizonyítsuk be, hogy $ AC \\ párhuzamos BD $.

Adott: $ AO \u003d OB $, $ CO \u003d OD $.

Bizonyít: $ AC \\ párhuzamos BD $.

Bizonyíték.

A $ AO \u003d OB $, $ CO \u003d OD $ feladat feltételéből és a $ ∠1 \u003d ∠2 $ függőleges szögek egyenlőségéből a háromszögek egyenlőségének I. kritériuma szerint következik, hogy $ \\ bigtriangleup COA \u003d \\ bigtriangleup DOB $. Így $ ∠3 \u003d ∠4 $.

A $ 3 $ és a $ 4 $ szögek kereszteződnek a két AC AC $ és $ BD $ vonalnál és egy szekundáns $ AB $ vonalnál. Ezután a $ AC \\ párhuzamos BD $ vonalak párhuzamosságának I. kritériuma szerint. Az állítás bebizonyosodott.

2. példa

Adott szög $ ∠2 \u003d 45 ^ (\\ circ) $, és $ ∠7 $ $ 3 $ szorosa az adott szögnek. Bizonyítsuk be, hogy $ a \\ párhuzamos b $.

Adott: $ ∠2 \u003d 45 ^ (\\ circ) $, $ ∠7 \u003d 3∠2 $.

Bizonyít: $ a \\ párhuzamos b $.

Bizonyíték:

Keresse meg a $ 7 $ szög értékét:

$ ∠7 \u003d 3 \\ cdot 45 ^ (\\ circ) \u003d 135 ^ (\\ circ) $.

Függőleges szögek $ ∠5 \u003d ∠7 \u003d 135 ^ (\\ circ) $, $ ∠2 \u003d ∠4 \u003d 45 ^ (\\ circ) $.
Keresse meg a $ ∠5 + ∠4 \u003d 135 ^ (\\ circ) +45 ^ (\\ circ) \u003d 180 ^ (\\ circ) $ belső szögek összegét.

A $ a \\ párhuzamos b $ egyenesek párhuzamosságának harmadik kritériuma szerint. Az állítás bebizonyosodott.

3. példa

Adott: $ \\ bigtriangleup ABC \u003d \\ bigtriangleup ADB $.

Bizonyít: $ AC \\ párhuzamos BD $, $ AD \\ párhuzamos BC $.

Bizonyíték:

A vizsgált számadatok közös oldala $ AB $.

Mivel a $ ABC $ és $ ADB $ háromszögek egyenlőek, akkor $ AD \u003d CB $, $ AC \u003d BD $, és a megfelelő szögek megegyeznek $ ∠1 \u003d ∠2 $, $ ∠3 \u003d ∠4 $, $ ∠5 \u003d ∠6 $.

A $ 3 $ és a $ 4 $ szög párja - keresztben fekszik a $ AC $ és $ BD $ egyenesek és a megfelelő szekunder $ AB $ szempontjából, tehát az egyenesek párhuzamosságának I. kritériuma szerint $ AC \\ párhuzamos BD $.

A $ 5 $ és a $ 6 $ szögek keresztezik egymást a $ AD $ és $ BC $ vonalak és a megfelelő szekunder $ AB $, ezért a $ AD \\ párhuzamos BC $ párhuzamosság I. kritériuma szerint.

Ez a cikk a párhuzamos és párhuzamos vonalakról szól. Először megadjuk a párhuzamos vonalak definícióját síkban és térben, megjelöléseket vezetünk be, példákat és grafikus ábrákat adunk a párhuzamos vonalakról. Ezenkívül elemezzük az egyenes vonalak párhuzamosságának jeleit és feltételeit. A konklúzióban tipikus problémák megoldásait mutatjuk be az egyenesek párhuzamosságának bizonyítására, amelyeket egyenes egyenletei adnak meg egy téglalap alakú koordinátarendszerben egy síkban és háromdimenziós térben.

Oldal navigáció.

Párhuzamos vonalak - alapvető információk.

Meghatározás.

Két síkot egy síknak nevezünk párhuzamosha nincsenek közös pontjaik.

Meghatározás.

A háromdimenziós térben két egyeneset hívunk párhuzamosha ugyanabban a síkban fekszenek és nincsenek közös pontjaik.

Megjegyezzük, hogy az "ha egy síkban fekszenek" tagmondat a térben a párhuzamos vonalak meghatározásában nagyon fontos. Tisztázzuk ezt a pontot: a háromdimenziós térben két olyan egyenes, amelynek nincsenek közös pontjai és nem ugyanazon a síkon fekszenek, nem párhuzamosak, hanem keresztezik egymást.

Íme néhány példa a párhuzamos vonalakra. A notebook lap ellentétes szélei párhuzamos egyenes vonalakon helyezkednek el. Azok az egyenes vonalak, amelyek mentén a ház falának síkja keresztezi a mennyezet és a padló síkját, párhuzamosak. A vízszintes talajú vasúti sínek párhuzamos egyeneseknek tekinthetők.

A párhuzamos vonalak jelölésére használja a "" szimbólumot. Vagyis, ha az a és b egyenesek párhuzamosak, akkor röviden írhatunk egy b-t.

Megjegyzés: ha az a és b egyenesek párhuzamosak, akkor azt mondhatjuk, hogy az a egyenes párhuzamos a b vonallal, és azt is, hogy a b egyenes párhuzamos az a vonallal.

Fogalmazzunk meg egy olyan állítást, amely fontos szerepet játszik a síkon lévő párhuzamos vonalak tanulmányozásában: egy olyan ponton keresztül, amely nem egy adott vonalon fekszik, egyetlen egy vonal áll párhuzamosan az adott vonallal. Ezt az állítást ténynek vesszük (a planimetria ismert axiómái alapján nem bizonyítható), és párhuzamos vonalak axiómájának nevezzük.

A térbeli esetre a következő tétel érvényes: a tér bármely olyan pontján keresztül, amely nem egy adott egyenesen fekszik, egyetlen egyenes áll párhuzamosan az adott egyennel. Ez a tétel könnyen igazolható a párhuzamos vonalak fenti axiómájának felhasználásával (bizonyítékát megtalálhatja a 10-11. Évfolyamok geometriai tankönyvében, amelyet a cikk végén a bibliográfia mutat be).

A térbeli esetre a következő tétel igaz: a tér bármely olyan pontján keresztül, amely nem egy adott egyenesen fekszik, egyetlen egyenes áll párhuzamosan az adott egyenessel. Ez a tétel könnyen igazolható a párhuzamos vonalak fenti axiómájával.

Az egyenes vonalak párhuzamossága - a párhuzamosság jelei és feltételei.

Az egyenes vonalak párhuzamossága elegendő feltétel a vonalak párhuzamosságához, vagyis olyan feltétel, amelynek teljesítése garantálja a vonalak párhuzamosságát. Más szavakkal, ennek a feltételnek a teljesítése elegendő az egyenesek párhuzamosságának tényének megállapításához.

Szükséges és elégséges feltételek vannak az egyenesek párhuzamosságához a síkon és a háromdimenziós térben is.

Tisztázzuk a "párhuzamos vonalak szükséges és elégséges feltétele" kifejezés jelentését.

Kiderítettük már az egyenesek párhuzamosságának elegendő feltételét. De mi az "egyenes vonalak párhuzamosságának szükséges feltétele"? A "szükséges" néven egyértelmű, hogy ennek a feltételnek a teljesítése szükséges az egyenesek párhuzamosságához. Más szavakkal, ha a vonalak párhuzamosságához szükséges feltétel nem teljesül, akkor a vonalak nem párhuzamosak. Ily módon szükséges és elegendő feltétel a vonalak párhuzamosságához Olyan feltétel, amelynek teljesítése egyszerre szükséges és elegendő az egyenesek párhuzamosságához. Vagyis egyrészt ez az egyenesek párhuzamosságának jele, másrészt olyan tulajdonság, amely a párhuzamos egyenesekkel rendelkezik.

Az egyenesek párhuzamosságához szükséges és elégséges feltétel megfogalmazása előtt ajánlatos több segéddefiníciót felidézni.

Secant vonal Olyan vonal, amely metszi a két megadott, nem egybeeső vonalat.

Amikor két egyenes szekund keresztezi egymást, nyolc fejletlen képződik. A vonalak párhuzamosságához szükséges és elégséges feltétel megfogalmazásában az ún áthúzódó, megfelelő és egyoldalú sarkok... Mutassuk meg őket a rajzon.

Tétel.

Ha a síkon két egyeneset metsz egy metszéspont, akkor a párhuzamosságuk érdekében szükséges és elegendő, ha a keresztbe eső szögek egyenlőek, vagy a megfelelő szögek egyenlőek, vagy az egyoldalas szögek összege 180 fok.

Mutassunk egy grafikus ábrát erről a síkban az egyenes vonalak párhuzamosságának szükséges és elegendő feltételéről.

Az egyenes vonalak párhuzamosságának ezen körülményeiről bizonyítékokat találhat a 7-9. Osztályú geometriai tankönyvekben.

Ne feledje, hogy ezeket a feltételeket háromdimenziós térben is lehet használni - a lényeg az, hogy a két vonal és a másodlagos azonos síkban feküdjön.

Íme még néhány tétel, amelyeket gyakran használnak a vonalak párhuzamosságának bizonyítására.

Tétel.

Ha a síkban két egyenes párhuzamos a harmadik egyenessel, akkor párhuzamosak. Ennek a kritériumnak a bizonyítása a párhuzamos vonal axiómájából következik.

Hasonló feltétel van az egyenes vonalak párhuzamosságára a háromdimenziós térben.

Tétel.

Ha a térben két vonal párhuzamos a harmadik vonallal, akkor párhuzamosak. Ennek a jelnek a bizonyítékát a 10. osztály geometriai óráin veszik figyelembe.

Szemléltessük a megadott tételeket.

Bemutassunk még egy tételt, amely lehetővé teszi a síkok egyenesének párhuzamosságának bizonyítását.

Tétel.

Ha a síkban két egyenes merőleges a harmadik egyenesre, akkor párhuzamosak.

Hasonló tétel létezik a térbeli vonalakra is.

Tétel.

Ha a háromdimenziós térben két egyenes merőleges egy síkra, akkor párhuzamosak.

Ábrázoljuk ezeknek a tételeknek megfelelő ábrákat.

Az összes fent megfogalmazott tétel, kritérium, valamint szükséges és elégséges feltétel kiválóan alkalmas a vonalak párhuzamosságának bizonyítására a geometria módszereivel. Vagyis két adott vonal párhuzamosságának igazolásához meg kell mutatni, hogy párhuzamosak a harmadik vonallal, vagy meg kell mutatni a metsző szögek egyenlőségét stb. Sok hasonló problémát megoldanak a gimnázium geometriai óráin. Meg kell azonban jegyezni, hogy sok esetben kényelmes a koordináta-módszer alkalmazása az egyenesek párhuzamosságának igazolására síkban vagy háromdimenziós térben. Fogalmazzuk meg az egyenesek párhuzamosságához szükséges és elégséges feltételeket, amelyek téglalap alakú koordinátarendszerben vannak megadva.

Vonalak párhuzama téglalap alakú koordinátarendszerben.

A cikk ezen a pontján megfogalmazzuk szükséges és elégséges feltételek a vonalak párhuzamosságához téglalap alakú koordináta-rendszerben, az ezeket az egyeneseket meghatározó egyenletek formájától függően, és a tipikus problémákra is részletes megoldásokat adunk.

Kezdjük az Oxy téglalap alakú koordinátarendszer síkján lévő két egyenes párhuzamosságának feltételével. Bizonyítása az egyenes irányító vektorának és a síkban lévő egyenes normálvektorának meghatározásán alapul.

Tétel.

Két nem egybeeső egyenes párhuzamosságához a síkon szükségszerű és elegendő, ha ezen egyenesek irányvektorai kollineárisak, vagy ezen egyenesek normálvektorai kollinárisak, vagy az egyik egyenes irányvektora merőleges a második egyenes normálvektorára.

Nyilvánvaló, hogy a sík két egyenesének párhuzamossága a következőre csökken: (az egyenesek irányvektorai vagy az egyenesek normálvektorai) vagy (az egyik egyenes irányvektorai és a második egyenes normálvektorai). Tehát, ha az a és b egyenesek irányvektorai, és és az a és a b egyenes normális vektorai, akkor az a és b egyenesek párhuzamosságának szükséges és elegendő feltétele írható , vagy , vagy ahol t valamilyen valós szám. Viszont az a és b egyenesek vezetőinek és (vagy) normál vektorainak koordinátáit az egyenesek ismert egyenleteiből találjuk meg.

Különösen akkor, ha a sík Oxy téglalap alakú koordinátarendszerében az a egyeneset a forma egyenesének általános egyenlete határozza meg és b vonal - , akkor ezeknek a vonalaknak a normál vektorai rendelkeznek koordinátákkal, illetve az a és b egyenesek párhuzamosságának feltételeit írjuk.

Ha az a egyenes megfelel az alakzat meredekségével egyenes vonal egyenletének és a b egyenesnek, akkor ezen egyenesek normálvektorainak vannak koordinátái és, és ezen egyenesek párhuzamosságának feltétele ... Ezért, ha a téglalap alakú koordinátarendszer síkján lévő egyenesek párhuzamosak és lejtési együtthatójú egyenesek egyenleteivel megadhatók, akkor az egyenesek meredekségi együtthatói megegyeznek. És fordítva: ha a téglalap alakú koordinátarendszer síkján a nem egyező vonalakat meg lehet határozni egyenlő meredekségi együtthatójú egyenletek egyenleteivel, akkor az ilyen egyenesek párhuzamosak.

Ha a téglalap alakú koordinátarendszerben az a egyenes és a b egyenes egyenes vonal kanonikus egyenletei határozzák meg az alak síkjában és , vagy egy egyenes paraméteres egyenletei a forma síkján és ennek megfelelően ezeknek az egyeneseknek az irányvektorai rendelkeznek koordinátákkal, és az a és b egyenesek párhuzamosságának feltételét így írjuk.

Elemezzük több példa megoldásait.

Példa.

A vonalak párhuzamosak? és?

Döntés.

Átírjuk az egyenes egyenletét szakaszokban egy egyenes általános egyenletének formájában: ... Most láthatja, hogy ez a vonal normális vektora , a az egyenes normálvektora. Ezek a vektorok nem egyenesek, mivel nincs valós t szám, amelyre az egyenlőség ( ). Következésképpen a síkbeli vonalak párhuzamosságának szükséges és elégséges feltétele nem teljesül, ezért az adott egyenesek nem párhuzamosak.

Válasz:

Nem, a vonalak nem párhuzamosak.

Példa.

Egyenesek és párhuzamosak?

Döntés.

Vigyük el az egyenes kanonikus egyenletét az egyenes és a lejtő egyenletére :. Nyilvánvaló, hogy az egyenesek egyenletei nem azonosak (ebben az esetben az adott egyenesek azonosak lennének) és az egyenesek meredekségei megegyeznek, ezért az eredeti egyenesek párhuzamosak.

Második megoldás.

Először megmutatjuk, hogy az eredeti vonalak nem esnek egybe: vegyük a vonal bármely pontját, például (0, 1), ennek a pontnak a koordinátái nem felelnek meg a vonal egyenletének, ezért a vonalak nem esnek egybe. Most ellenőrizzük e vonalak párhuzamosságának feltételét. Az egyenes normálvektora vektor, az egyenes irányvektora pedig vektor. Számítsuk ki és: ... Következésképpen a vektorok és merőlegesek, ami azt jelenti, hogy az adott vonalak párhuzamosságának szükséges és elégséges feltétele teljesül. Így a vonalak párhuzamosak.

Válasz:

A megadott vonalak párhuzamosak.

Az egyenesek párhuzamosságának igazolására egy téglalap alakú koordináta-rendszerben háromdimenziós térben a következő szükséges és elegendő feltételt kell használni.

Tétel.

A háromdimenziós térben az egymással nem egyező vonalak párhuzamosságához szükséges és elegendő, hogy irányvektoraik kollineárisak legyenek.

Tehát, ha ismertek a háromdimenziós térben lévő téglalap alakú koordinátarendszerben az egyenesek egyenletei, és meg kell válaszolni a kérdést, hogy ezek az egyenesek párhuzamosak-e vagy sem, akkor meg kell találnia ezen egyenesek irányvektorainak koordinátáit, és ellenőriznie kell, hogy az irányvektorok kollinearitásának feltétele teljesül-e. Más szóval, ha és - egyenes vonalak irányvektorai a megadott egyenesek koordinátái és. Mivel akkor. Így teljesül a két egyenes térbeli párhuzamosságának szükséges és elégséges feltétele. Ez bizonyítja a vonalak párhuzamosságát és .

Hivatkozások felsorolása.

Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Poznyak E.G., Yudina I.I. Geometria. 7 - 9 évfolyam: tankönyv oktatási intézmények számára.
Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometria. Tankönyv a középiskola 10–11.
Pogorelov A.V., Geometria. Tankönyv az oktatási intézmények 7–11.
Bugrov Y.S., Nikolsky S.M. Felsõbb matematika. Első kötet: A lineáris algebra és az analitikus geometria elemei.
Ilyin V.A., Poznyak E.G. Analitikai geometria.

Ebben a cikkben párhuzamos vonalakról fogunk beszélni, definíciókat adunk, jelöljük a párhuzamosság jeleit és feltételeit. Az elméleti anyag érthetősége érdekében illusztrációkat és tipikus példák megoldását fogjuk használni.

1. meghatározás

Párhuzamos vonalak egy síkon - két egyenes egy síkon, amelynek nincsenek közös pontjai.

2. definíció

Párhuzamos vonalak a háromdimenziós térben - két egyenes háromdimenziós térben, ugyanabban a síkban fekszik és nincsenek közös pontjai.

Meg kell jegyezni, hogy a párhuzamos egyenesek meghatározásához a térben rendkívül fontos tisztázni az "azonos síkban fekvő" pontot: a háromdimenziós térben két olyan egyenes, amelynek nincsenek közös pontjai és nem ugyanazon a síkon fekszenek, nem párhuzamosak, hanem keresztezik egymást.

A vonalak párhuzamosságának jelzésére általános a symbol szimbólum használata. Vagyis ha az adott a és b egyenes párhuzamos, akkor ezt a feltételt röviden a következőképpen kell megírni: a ‖ b. Szavakkal a vonalak párhuzamosságát a következőképpen jelöljük: az a és b egyenes párhuzamos, vagy az a egyenes párhuzamos a b vonallal, vagy a b egyenes párhuzamos az a vonallal.

Fogalmazzunk meg egy olyan állítást, amely fontos szerepet játszik a vizsgált témában.

Alapigazság

Az egyetlen egyenes, amely párhuzamos az adottval, egy olyan ponton halad át, amely nem tartozik az adott vonalhoz. Ez az állítás a planimetria ismert axiómái alapján nem bizonyítható.

Abban az esetben, amikor térről beszélünk, a tétel igaz:

1. tétel

A tér bármely olyan pontján keresztül, amely nem tartozik egy adott egyeneshez, egyetlen egyenes lesz párhuzamos az adott ponttal.

Ezt a tételt könnyű bizonyítani a fenti axióma (10-11 osztályú geometriai program) alapján.

A párhuzamossági kritérium elegendő feltétel, amely mellett az egyenesek párhuzamossága garantált. Más szavakkal, ennek a feltételnek a teljesítése elegendő a párhuzamosság tényének megerősítéséhez.

Különösen vannak szükséges és elégséges feltételek az egyenesek párhuzamosságához a síkon és az űrben. Tisztázzuk: a szükséges azt a feltételt jelenti, amelynek teljesítése szükséges az egyenesek párhuzamosságához; ha nem teljesül, akkor a vonalak nem párhuzamosak.

Összefoglalva: az egyenesek párhuzamosságának szükséges és elégséges feltétele egy olyan feltétel, amelynek betartása szükséges és elegendő ahhoz, hogy az egyenesek párhuzamosak legyenek egymással. Ez egyrészt a párhuzamosság jele, másrészt a párhuzamos vonalakban rejlő tulajdonság.

Mielőtt pontos megfogalmazást adnánk a szükséges és elégséges feltételről, idézzünk fel még néhány további fogalmat.

3. definíció

Secant vonal - egy egyenes, amely metszi a két meghatározott, nem egybeeső egyeneset.

Két egyeneset keresztezve a szekán nyolc fejletlen sarkot képez. A szükséges és elegendő feltétel megfogalmazásához olyan típusú szögeket fogunk használni, mint keresztbe fekvő, megfelelő és egyoldalú. Bemutassuk őket szemléltetéssel:

2. tétel

Ha egy síkban két egyenes metszi a szekántot, akkor ahhoz, hogy az adott egyenesek párhuzamosak legyenek, szükséges és elegendő, hogy a keresztbe eső szögek egyenlőek legyenek, vagy a megfelelő szögek egyenlőek legyenek, vagy az egyoldalas szögek összege 180 fok.

Grafikusan szemléltessük a síkban az egyenes vonalak párhuzamosságának szükséges és elégséges feltételét:

Ezeknek a feltételeknek a bizonyítéka megtalálható a 7-9. Osztály geometriai programjában.

Általában ezek a feltételek a háromdimenziós térre alkalmazhatók, tekintettel arra, hogy két vonal és egy szekundáns vonal ugyanahhoz a síkhoz tartozik.

Jelöljünk még néhány olyan tételt, amelyeket gyakran használnak a vonalak párhuzamosságának tényének bizonyításában.

3. tétel

Egy síkban két, a harmadikkal párhuzamos egyenes párhuzamos egymással. Ezt a kritériumot a párhuzamosság fentebb jelzett axiómája bizonyítja.

4. tétel

A háromdimenziós térben két, a harmadikkal párhuzamos egyenes párhuzamos egymással.

Az attribútum igazolását a 10. osztály geometriai programja tanulmányozza.

Hadd szemléltessük ezeket a tételeket:

Emeljünk ki még egy pár tételt, amelyek bizonyítják a vonalak párhuzamosságát.

5. tétel

A síkon két, a harmadikra \u200b\u200bmerőleges egyenes párhuzamos egymással.

Fogalmazzunk meg hasonlót a háromdimenziós térre.

6. tétel

A háromdimenziós térben a harmadikra \u200b\u200bmerőleges két egyenes párhuzamos egymással.

Illusztráljuk:

A fenti tételek, kritériumok és feltételek mindegyike lehetővé teszi az egyenesek párhuzamosságának kényelmes bizonyítását geometriai módszerekkel. Vagyis az egyenesek párhuzamosságának bizonyítása érdekében meg lehet mutatni, hogy a megfelelő szögek egyenlőek, vagy azt a tényt, hogy két adott egyenes merőleges a harmadikra \u200b\u200bstb. De vegye figyelembe, hogy gyakran kényelmesebb a koordináta-módszer segítségével igazolni az egyenesek párhuzamosságát síkban vagy háromdimenziós térben.

Vonalak párhuzama téglalap alakú koordinátarendszerben

Egy adott téglalap alakú koordináta-rendszerben az egyeneset a lehetséges típusok egyikének síkján lévő egyenes egyenlete határozza meg. Hasonlóképpen, a háromdimenziós térben egy téglalap alakú koordinátarendszerben megadott egyenes megfelel a tér egyenesének néhány egyenletének.

Írjuk fel az egyenesek párhuzamosságának szükséges és elégséges feltételeit egy téglalap alakú koordináta-rendszerben, az adott egyeneseket leíró egyenlet típusától függően.

Kezdjük a síkok vonalainak párhuzamosságának feltételével. Alapja egy egyenes irányvektorának és egy síkban lévő egyenes normálvektorának meghatározása.

7. tétel

Ahhoz, hogy két nem egybeeső egyenes párhuzamos legyen a síkon, szükséges és elegendő, hogy az adott egyenesek irányvektorai kollinárisak legyenek, vagy az adott egyenesek normálvektorai kollineárisak legyenek, vagy az egyik egyenes irányvektora merőleges legyen a másik egyenes normálvektorára.

Nyilvánvalóvá válik, hogy a síkban az egyenes vonalak párhuzamosságának feltétele kollináris vektorok állapotán vagy két vektor merőlegességének feltételén alapul. Vagyis ha a → \u003d (a x, a y) és b → \u003d (b x, b y) az a és b egyenesek irányvektorai;

és nb → \u003d (nbx, nby) az a és b egyenes normálvektorai, akkor a fenti szükséges és elégséges feltételt a következőképpen írjuk: a → \u003d t b → ⇔ ax \u003d t bxay \u003d t vagy na → \u003d t nb → ⇔ nax \u003d t nbxnay \u003d t nby vagy a →, nb → \u003d 0 ⇔ ax nbx + ay nby \u003d 0, ahol t valamilyen valós szám. Az irány- vagy közvetlen vektor koordinátáit az egyenesek megadott egyenletei határozzák meg. Nézzünk meg néhány alapvető példát.

Az a egyeneset egy téglalap alakú koordinátarendszerben az egyenes általános egyenlete határozza meg: A 1 x + B 1 y + C 1 \u003d 0; b vonal - A 2 x + B 2 y + C 2 \u003d 0. Ekkor az adott vonalak normálvektorainak koordinátái lesznek (A 1, B 1) és (A 2, B 2). A párhuzamossági feltétel a következőképpen íródik:

A 1 \u003d t A 2 B 1 \u003d t B 2

Az a egyeneset az egyenes és az y \u003d k 1 x + b 1 forma meredekségének egyenlete írja le. B vonal - y \u003d k 2 x + b 2. Ekkor az adott egyenesek normál vektorainak koordinátái (k 1, - 1) és (k 2, - 1) lesznek, és a párhuzamossági feltételt a következőképpen írjuk:

k 1 \u003d t k 2 - 1 \u003d t (- 1) ⇔ k 1 \u003d t k 2 t \u003d 1 ⇔ k 1 \u003d k 2

Ha tehát egy téglalap alakú koordináta-rendszer síkján lévő párhuzamos vonalakat lejtési együtthatójú egyenletek adják meg, akkor az adott egyenesek meredekségei egyenlőek lesznek. És az ellenkező állítás igaz: ha a téglalap alakú koordinátarendszer síkján a nem egyező vonalakat egy egyenes egyenletei azonos meredekség-együtthatókkal határozzák meg, akkor ezek az adott egyenesek párhuzamosak.

A téglalap alakú koordináta-rendszerben az a és b vonalakat a síkban lévő egyenes kanonikus egyenletei adják meg: x - x 1 ax \u003d y - y 1 ay és x - x 2 bx \u003d y - y 2 a síkban lévő egyenes vonalának paraméteres egyenleteivel: x \u003d x 1 + λ axy \u003d y 1 + λ ay és x \u003d x 2 + λ bxy \u003d y 2 + λ.

Ekkor az adott vonalak irányvektorai a következők lesznek: a x, a y és b x, b y, és a párhuzamossági feltétel a következőképpen íródik:

a x \u003d t b x a y \u003d t b y

Nézzünk meg néhány példát.

1. példa

Két egyenes adható: 2 x - 3 y + 1 \u003d 0 és x 1 2 + y 5 \u003d 1. Meg kell határozni, hogy párhuzamosak-e.

Döntés

Az egyenes egyenletét szakaszokba írjuk általános egyenlet formájában:

x 1 2 + y 5 \u003d 1 ⇔ 2 x + 1 5 y - 1 \u003d 0

Látjuk, hogy n a → \u003d (2, - 3) a 2 x - 3 y + 1 \u003d 0 egyenes normálvektora, és n b → \u003d 2, 1 5 az x 1 2 + y 5 \u003d 1 egyenes normálvektora.

Az így kapott vektorok nem kollineárisak, mivel nincs t értéke, amelyre az egyenlőség igaz lesz:

2 \u003d t 2 - 3 \u003d t 1 5 ⇔ t \u003d 1 - 3 \u003d t 1 5 ⇔ t \u003d 1 - 3 \u003d 1 5

Így a síkban az egyenesek párhuzamosságának szükséges és elégséges feltétele nem teljesül, ami azt jelenti, hogy az adott vonalak nem párhuzamosak.

Válasz: az adott vonalak nem párhuzamosak.

2. példa

Az y \u003d 2 x + 1 és x 1 \u003d y - 4 2 egyeneseket megadjuk. Párhuzamosak?

Döntés

Konvertálja az x 1 \u003d y - 4 2 egyenes kanonikus egyenletét a meredekségű egyenes egyenletére:

x 1 \u003d y - 4 2 ⇔ 1 (y - 4) \u003d 2 x ⇔ y \u003d 2 x + 4

Látjuk, hogy az y \u003d 2 x + 1 és y \u003d 2 x + 4 egyenesek egyenletei nem azonosak (ha másképp lenne, akkor a vonalak azonosak lennének), és a vonalak meredeksége megegyezik, ami azt jelenti, hogy az adott egyenesek párhuzamosak.

Próbáljuk másként megoldani a problémát. Először ellenőrizzük, hogy az adott sorok egybeesnek-e. Az y \u003d 2 x + 1 egyenes bármely pontját használjuk, például (0, 1), ennek a pontnak a koordinátái nem felelnek meg az x 1 \u003d y - 4 2 egyenes egyenletének, ezért az egyenesek nem esnek egybe.

A következő lépés a párhuzamossági feltétel teljesülésének meghatározása az adott vonalakra.

Az y \u003d 2 x + 1 egyenes normálvektora az n a → \u003d (2, - 1) vektor, a második megadott egyenes irányvektora pedig b → \u003d (1, 2). Ezeknek a vektoroknak a skaláris szorzata nulla:

n a →, b → \u003d 2 1 + (- 1) 2 \u003d 0

Így a vektorok merőlegesek: ez megmutatja számunkra az eredeti egyenesek párhuzamosságához szükséges és elégséges feltétel teljesülését. Azok. az adott vonalak párhuzamosak.

Válasz: az adott vonalak párhuzamosak.

A háromdimenziós tér téglalap alakú koordinátarendszerében a vonalak párhuzamosságának igazolásához a következő szükséges és elégséges feltételt használjuk.

8. tétel

Ahhoz, hogy a háromdimenziós térben két, nem egybeeső egyenes párhuzamos legyen, szükséges és elegendő, hogy ezen egyenesek irányvektorai kollineárisak legyenek.

Azok. a háromdimenziós térben adott egyenesek adott egyenleteire a kérdésre adott válasz: vajon párhuzamosak-e vagy sem, az adott egyenesek irányvektorainak koordinátáinak meghatározásával, valamint kollinearitásuk állapotának ellenőrzésével adódik. Más szavakkal, ha a → \u003d (ax, ay, az) és b → \u003d (bx, by, bz) az a és b egyenes irányvektorai, akkor ahhoz, hogy párhuzamosak legyenek, léteznie kell egy ilyen valós számnak, hogy az egyenlőség érvényesüljön:

a → \u003d t b → ⇔ a x \u003d t b x a y \u003d t b y a z \u003d t b z

3. példa

Az x 1 \u003d y - 2 0 \u003d z + 1 - 3 és x \u003d 2 + 2 λ y \u003d 1 z \u003d - 3 - 6 λ egyenesek. Bizonyítani kell e vonalak párhuzamosságát.

Döntés

A feladat feltételei egy egyenes kanonikus egyenleteit állítják be a térben, egy másik egyenesek paraméteres egyenleteit a térben. Irányvektorok a → és b → az adott egyeneseknek koordinátái vannak: (1, 0, - 3) és (2, 0, - 6).

1 \u003d t 2 0 \u003d t 0 - 3 \u003d t - 6 ⇔ t \u003d 1 2, akkor a → \u003d 1 2 b →.

Következésképpen a vonalak térbeli párhuzamosságának szükséges és elégséges feltétele teljesül.

Válasz: az adott vonalak párhuzamossága bebizonyosodott.

Ha hibát észlel a szövegben, válassza ki azt, és nyomja meg a Ctrl + Enter billentyűt