Egyes alakzatok súlypontjának helyzete. Lapos alakzatok súlypontjának koordinátáinak meghatározása Szabálytalan alakú lapos test súlypontjának meghatározása

A fent kapott általános képletek alapján lehetőség van konkrét módszerek megjelölésére a testek súlypontjainak koordinátáinak meghatározására.

1. Szimmetria. Ha egy homogén testnek van síkja, tengelye vagy szimmetriaközéppontja (7. ábra), akkor a súlypontja a szimmetriasíkban, a szimmetriatengelyben vagy a szimmetriaközéppontban van.

7. ábra

2. Hasítás. A test véges számú részre van osztva (8. ábra), amelyek mindegyikénél ismert a súlypont helyzete és a terület.

8. ábra

3.A negatív területek módszere. A particionálási módszer speciális esete (9. ábra). Kivágással rendelkező testekre vonatkozik, ha a kivágás nélküli test súlypontja és a kivágás ismert. A kivágott lemez formájú testet egy tömör lemez (kivágás nélkül) kombinációja képviseli, amelynek területe S 1 és a kivágott rész S 2 területe.

9. ábra

4.csoportosítási módszer. Jó kiegészítője az utolsó két módszernek. Az ábra alkotóelemeire bontása után kényelmes lehet néhányat újra kombinálni, hogy azután e csoport szimmetriájának figyelembevételével egyszerűsítsük a megoldást.

Egyes homogén testek súlypontjai.

1) Egy körív súlypontja. Vegye figyelembe az ívet AB sugár R központi szöggel. A szimmetria miatt ennek az ívnek a súlypontja a tengelyen fekszik Ökör(10. ábra).

10. ábra

Keressük meg a koordinátát a képlet segítségével. Ehhez válassza ki az íven AB elem MM' hossza , amelynek helyzetét a szög határozza meg . Koordináta x elem MM' fog . Ezeket az értékeket helyettesítve xés d lés szem előtt tartva, hogy az integrált az ív teljes hosszára kell kiterjeszteni, a következőt kapjuk:

ahol L- ívhossz AB, egyenlő .

Innentől végre azt találjuk, hogy a körív súlypontja a szimmetriatengelyén van a középponttól távol. RÓL RŐL egyenlő

ahol a szöget radiánban mérjük.

2) A háromszög területének súlypontja. Tekintsünk egy háromszöget, amely a síkban fekszik Oxy, melynek csúcskoordinátái ismertek: Ai(x i,y i), (én= 1,2,3). A háromszög oldalával párhuzamos keskeny csíkokra bontása DE 1 DE 2 , arra a következtetésre jutunk, hogy a háromszög súlypontjának a mediánhoz kell tartoznia DE 3 M 3 (11. ábra) .

11. ábra

A háromszög oldalával párhuzamos csíkokra bontása DE 2 DE 3 , akkor biztos lehet benne, hogy a mediánon kell feküdnie DE 1 M egy . Ily módon a háromszög súlypontja a mediánjainak metszéspontjában van, amely, mint tudod, elválasztja a harmadik részt minden mediántól, a megfelelő oldaltól számítva.

Különösen a medián esetében DE 1 M 1-et kapunk, mivel a pont koordinátái M 1 a csúcskoordináták számtani átlaga DE 2 és DE 3:

x c = x 1 + (2/3)∙(x M 1 - x 1) = x 1 + (2/3)∙[(x 2 + x 3)/2-x 1 ] = (x 1 +x 2 +x 3)/3.

Így a háromszög súlypontjának koordinátái a csúcsok koordinátáinak számtani átlagai:

x c =(1/3)Σ x i ; y c =(1/3)Σ y i.

3) A kör alakú szektor területének súlypontja. Tekintsünk egy kör sugarú szektorát R 2α középponti szöggel, a tengely körül szimmetrikusan helyezkedik el Ökör(12. ábra) .

Ez nyilvánvaló y c = 0, és a távolság annak a körnek a középpontjától, amelyből ez a szektor el van vágva a súlypontig, a következő képlettel határozható meg:

12. ábra

Ezt az integrált a legegyszerűbben úgy számíthatjuk ki, hogy az integrációs tartományt elemi szektorokra osztjuk egy szöggel dφ. Az első rendű végtelen kicsikig egy ilyen szektor helyettesíthető egy háromszöggel, amelynek alapja egyenlő R× dφ és magasság R. Egy ilyen háromszög területe dF=(1/2)R 2 ∙dφ, súlypontja pedig 2/3 távolságra van R felülről, így az (5)-be tesszük x = (2/3)R∙cosφ. Behelyettesítés (5) F= α R 2, kapjuk:

Az utolsó képlet segítségével kiszámítjuk különösen a súlypont távolságát félkör.

A (2)-ben α = π/2 behelyettesítve kapjuk: x c = (4R)/(3π) ≅ 0,4 R .

1. példa Határozzuk meg az ábrán látható homogén test súlypontját! 13.

13. ábra

A test homogén, két szimmetrikus formájú részből áll. Súlypontjuk koordinátái:

Köteteik:

Ezért a test súlypontjának koordinátái

2. példa Keresse meg a derékszögben meghajlított lemez súlypontját! Méretek - a rajzon (14. ábra).

14. ábra

Súlypont koordináták:

Négyzetek:

Rizs. 6.5.

3. példa Négyzet alakú lapból cm négyzet alakú lyukat vágunk ki (15. ábra). Keresse meg a lap súlypontját.

15. ábra

Ebben a problémában kényelmesebb a testet két részre osztani: egy nagy négyzetre és egy négyzet alakú lyukra. Csak a lyuk területét kell negatívnak tekinteni. Ezután a lap súlypontjának koordinátái a furattal:

koordináta mivel a testnek van szimmetriatengelye (átlója).

4. példa A huzaltartó (16. ábra) három azonos hosszúságú részből áll l.

16. ábra

A szakaszok súlypontjainak koordinátái:

Ezért a teljes konzol súlypontjának koordinátái:

5. példa Határozzuk meg a rácsozat súlypontjának helyzetét, amelynek minden rúdja azonos lineáris sűrűségű (17. ábra).

Emlékezzünk vissza, hogy a fizikában egy test ρ sűrűsége és g fajsúlya a következő összefüggéssel függ össze: γ= ρ g, ahol g- a gravitáció gyorsulása. Egy ilyen homogén test tömegének meghatározásához meg kell szoroznia a sűrűséget a térfogatával.

17. ábra

A "lineáris" vagy "lineáris" sűrűség kifejezés azt jelenti, hogy a rácsos rúd tömegének meghatározásához a lineáris sűrűséget meg kell szorozni a rúd hosszával.

A probléma megoldásához használhatja a particionálási módszert. Ha egy adott rácsot 6 különálló rúd összegeként ábrázolunk, a következőt kapjuk:

ahol L i hossz én-th rúd a gazdaság, és x i, y i súlypontjának koordinátái.

A probléma megoldása leegyszerűsíthető az utolsó 5 rácsos rudak csoportosításával. Könnyen belátható, hogy a negyedik rúd közepén elhelyezkedő szimmetriaközéppontú figurát alkotnak, ahol ennek a rúdcsoportnak a súlypontja található.

Így egy adott rácsos tartó csak két rúdcsoport kombinációjával ábrázolható.

Az első csoport az első rúdból áll L 1 = 4 m, x 1 = 0 m, y 1 = 2 m. A második rúdcsoport öt rúdból áll, amelyekhez L 2 = 20 m, x 2 = 3 m, y 2 = 2 m.

A gazdaság súlypontjának koordinátáit a következő képlet határozza meg:

x c = (L 1 ∙x 1 +L 2 ∙x 2)/(L 1 + L 2) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙y 1 +L 2 ∙y 2)/(L 1 + L 2) = (4,2 + 20,2)/24 = 2 m.

Vegye figyelembe, hogy a központ TÓL TŐL az összekötő vonalon fekszik TÓL TŐL 1 és TÓL TŐL 2, és felosztja a szakaszt TÓL TŐL 1 TÓL TŐL 2 kapcsolatban: TÓL TŐL 1 TÓL TŐL/SS 2 = (x c - x 1)/(x 2 - x c ) = L 2 /L 1 = 2,5/0,5.

Kérdések önvizsgálathoz

Mi a párhuzamos erők középpontja?

Hogyan határozzák meg a párhuzamos erők középpontjának koordinátáit?

Hogyan határozható meg a párhuzamos erők középpontja, amelyek eredője nulla?

Mi a tulajdonsága a párhuzamos erők középpontjának?

Milyen képletekkel számítjuk ki a párhuzamos erők középpontjának koordinátáit?

Mi a test súlypontja?

Miért tekinthetők párhuzamos erők rendszerének a Föld vonzási erői, amelyek a test egy pontjára hatnak?

Írja fel az inhomogén és homogén testek súlypontjának meghatározására szolgáló képletet, a síkszelvények súlypontjának meghatározására szolgáló képletet?

Írja fel az egyszerű geometriai alakzatok súlypontjának meghatározására szolgáló képletet: téglalap, háromszög, trapéz és fél kör?

Mit nevezünk a terület statikus momentumának?

Mondjon példát olyan testre, amelynek súlypontja a testen kívül található!

Hogyan használják a szimmetriatulajdonságokat a testek súlypontjának meghatározására?

Mi a negatív súlyozás módszerének lényege?

Hol található a körív súlypontja?

Milyen grafikus konstrukcióval lehet megkeresni a háromszög súlypontját?

Írja fel a képletet, amely meghatározza egy körszektor súlypontját!

A háromszög és egy körszektor súlypontját meghatározó képletek segítségével állítson elő hasonló képletet egy körszakaszra.

Milyen képletekkel számítják ki a homogén testek, síkidomok és egyenesek súlypontjainak koordinátáit?

Mit nevezünk egy lapos alakzat területének tengelyhez viszonyított statikus nyomatékának, hogyan számítják ki és milyen méretei vannak?

Hogyan határozható meg a terület súlypontjának helyzete, ha ismert az egyes részei súlypontjainak helyzete?

Milyen segédtételeket használnak a súlypont helyzetének meghatározására?

A téma viszonylag könnyen elsajátítható, de rendkívül fontos az anyagok szilárdsági menetének tanulmányozásakor. Itt a fő figyelmet a lapos és geometriai formák, valamint a szabványos hengerelt profilok problémáinak megoldására kell fordítani.

Kérdések az önkontrollhoz

1. Mi a párhuzamos erők középpontja?

A párhuzamos erők középpontja az a pont, amelyen az adott pontokban kifejtett párhuzamos erők eredő rendszerének egyenese áthalad, ezen erők térbeli irányának bármilyen változása mellett.

2. Hogyan találjuk meg a párhuzamos erők középpontjának koordinátáit?

A párhuzamos erők középpontjának koordinátáinak meghatározásához a Varignon-tételt használjuk.

Tengely relatív x

Mx(R) = ΣMx(Fk), - y C R = Σy kFk És y C = Σy kFk /Σ Fk .

Tengely relatív y

M y (R) = ΣM y (Fk), - x C R = Σx kFk És x C = Σx kFk /Σ Fk .

A koordináta meghatározásához z C , forgassa el az összes erőt 90°-kal úgy, hogy párhuzamosak legyenek a tengellyel y (1.5. ábra, b). Azután

M z (R) = ΣM z (Fk), - z C R = Σz kFk És z C = Σz kFk /Σ Fk .

Ezért a párhuzamos erők középpontjának sugárvektorának meghatározására szolgáló képlet alakot ölt

r C = Σr kFk /Σ Fk.

3. Mi a test súlypontja?

Gravitáció középpontja - egy szilárd testtel állandóan összefüggő pont, amelyen a test részecskéire ható gravitációs erők eredője áthalad a test bármely helyén a térben. Egy homogén, szimmetriaközépponttal rendelkező testnél (kör, golyó, kocka stb.) a súlypont a test szimmetriaközéppontjában található. A merev test súlypontjának helyzete egybeesik tömegközéppontjának helyzetével.

4. Hogyan találjuk meg a téglalap, háromszög, kör súlypontját?

A háromszög súlypontjának megtalálásához meg kell rajzolnia egy háromszöget - egy ábrát, amely három szegmensből áll, amelyek három ponton kapcsolódnak egymáshoz. Mielőtt megtalálná az ábra súlypontját, vonalzóval kell megmérnie a háromszög egyik oldalának hosszát. Az oldal közepére tegyen egy jelet, majd kösse össze a szemközti csúcsot és a szakasz közepét egy mediánnak nevezett vonallal. Ismételje meg ugyanezt az algoritmust a háromszög második oldalával, majd a harmadikkal. A munkád eredménye három medián lesz, amelyek egy pontban metszik egymást, és ez lesz a háromszög súlypontja. Ha meg kell határozni egy homogén szerkezetű kerek korong súlypontját, akkor először keresse meg a kör átmérőinek metszéspontját. Ez lesz ennek a testnek a súlypontja. Ha figyelembe vesszük az olyan figurákat, mint a labda, a karika és a homogén téglalap alakú paralelepipedon, akkor bátran kijelenthetjük, hogy a karika súlypontja az ábra közepén lesz, de pontjain kívül a labda súlypontja a gömb geometriai középpontja, ez utóbbi esetben pedig a súlypont egy téglalap alakú paralelepipedon metszésponti átlói.

5. Hogyan találjuk meg a sík összetett szakasz súlypontjának koordinátáit?

Felosztási módszer: ha egy lapos alak véges számú ilyen részre osztható, amelyek mindegyikére ismert a tömegközéppont helyzete, akkor a teljes ábra súlypontjának koordinátáit a képletek határozzák meg:

X C = ( s k x k) / S; Y C = ( s k y k) / S,

ahol x k, y k az ábra részeinek súlypontjainak koordinátái;

s k - területük;

S \u003d s k - a teljes ábra területe.

6. Súlypont

1. Milyen esetben elegendő egy koordinátát számítással meghatározni a súlypont meghatározásához?

Az első esetben a súlypont meghatározásához elegendő egy koordináta meghatározása A testet véges számú részre osztjuk, amelyek mindegyikére a súlypont helyzete C és terület S ismert. Például egy test síkra vetítése xOy (1. ábra) két sík figuraként ábrázolható területekkel S1 És S2 (S = S 1 + S 2 ). Ezen alakzatok súlypontjai a pontokon vannak C 1 (x 1 , y 1) És C 2 (x 2, y 2) . Ekkor a test súlypontjának koordinátái az

Mivel az ábrák középpontjai az y tengelyen vannak (x = 0), csak a koordinátát találjuk Minket.

2 Hogyan veszik figyelembe a 4. ábrán látható furat területét az ábra súlypontjának meghatározására szolgáló képletben?

Negatív tömeg módszer

Ez a módszer abból áll, hogy a szabad üregekkel rendelkező testet szilárdnak, a szabad üregek tömegét pedig negatívnak tekintjük. A test súlypontjának koordinátáinak meghatározására szolgáló képletek formája nem változik.

Így a szabad üregekkel rendelkező test súlypontjának meghatározásakor a felosztás módszerét kell alkalmazni, de az üregek tömegét negatívnak kell tekinteni.

van ötleted a párhuzamos erők középpontjáról és annak tulajdonságairól;

tud képletek lapos alakzatok súlypontjának koordinátáinak meghatározására;

képesnek lenni határozza meg az egyszerű geometriai formák és szabványos hengerelt profilok sík alakjainak súlypontjának koordinátáit.

A KINEMATIKA ÉS DINAMIKA ELEMEI
Egy pont kinematikájának tanulmányozása után ügyeljen arra, hogy egy pont egyenetlen és egyenletes egyenes vonalú mozgását mindig a normál (centripetális) gyorsulás jellemzi. Egy test transzlációs mozgásánál (amelyet bármely pontjának mozgása jellemez) egy pont kinematikájának összes képlete alkalmazható. A rögzített tengely körül forgó test szögértékeinek meghatározására szolgáló képletek teljes szemantikai analógiát mutatnak a transzlációsan mozgó test megfelelő lineáris értékeinek meghatározására szolgáló képletekkel.

Téma 1.7. Pontkinematika
A téma tanulmányozásakor ügyeljen a kinematika alapfogalmaira: gyorsulás, sebesség, út, távolság.

Kérdések az önkontrollhoz

1. Mi a nyugalom és a mozgás fogalmának relativitása?

A mechanikai mozgás egy test vagy (részei) térbeli mozgásának időbeli változása a többi testhez képest. Az eldobott kő repülése, a kerék forgása a mechanikai mozgás példái.

2. Határozza meg a kinematika alapfogalmait: pálya, távolság, út, sebesség, gyorsulás, idő!

A sebesség egy pont mozgásának kinematikai mértéke, amely a térbeli helyzetében bekövetkezett változás sebességét jellemzi. A sebesség vektormennyiség, azaz nem csak a modul (skaláris komponens), hanem a térbeli irány is jellemzi.

A fizikából ismeretes, hogy egyenletes mozgás esetén a sebesség az egységnyi idő alatt megtett út hosszával határozható meg: v = s / t = const (feltételezzük, hogy az út origója és az idő egybeesik). Egyenes irányú mozgásnál a sebesség mind abszolút értékben, mind irányban állandó, vektora egybeesik a pályával.

A sebesség mértékegysége a rendszerben SI a hossz/idő arány határozza meg, azaz m/s.

A gyorsulás egy időpont sebességének változásának kinematikai mértéke. Más szóval, a gyorsulás a sebesség változásának mértéke.
A sebességhez hasonlóan a gyorsulás is vektormennyiség, vagyis nemcsak a modul, hanem a térbeli irány is jellemzi.

Az egyenes vonalú mozgásnál a sebességvektor mindig egybeesik a pályával, ezért a sebességváltozás vektora is egybeesik a pályával.

A fizika tananyagából ismert, hogy a gyorsulás a sebesség időegységenkénti változása. Ha rövid ideig Δt a pont sebessége Δv-vel változott, akkor az átlagos gyorsulás erre az időtartamra: a cp = Δv/Δt.

Az átlagos gyorsulás nem ad képet a sebességváltozás valódi nagyságáról az egyes időpillanatokban. Ugyanakkor nyilvánvaló, hogy minél rövidebb a vizsgált időtartam, amely alatt a sebességváltozás bekövetkezett, annál közelebb lesz a gyorsulás értéke a valódihoz (pillanatnyi).
Innen a definíció: a valódi (pillanatnyi) gyorsulás az a határ, amelyre az átlagos gyorsulás hajlik, amikor Δt nullára hajlik:

a = lim a cf t→0-nál vagy lim Δv/Δt = dv/dt.

Tekintettel arra, hogy v \u003d ds / dt, a következőt kapjuk: a \u003d dv / dt \u003d d 2 s / dt 2.

Az egyenes vonalú mozgás valódi gyorsulása egyenlő a sebesség első deriváltjával vagy a koordináta második deriváltjával (a mozgás kezdőpontjától való távolság) az idő függvényében. A gyorsulás mértékegysége a méter osztva egy másodperc négyzetével (m/s 2).

Röppálya- egy vonal a térben, amely mentén egy anyagi pont mozog.
Út az út hossza. A megtett út l egyenlő a test által bizonyos t idő alatt megtett pálya ívének hosszával. Az útvonal skaláris érték.

Távolság meghatározza egy pont helyzetét a pályáján, és valamilyen origóból mérik. A távolság algebrai mennyiség, hiszen a pont origóhoz viszonyított helyzetétől és a távolságtengely elfogadott irányától függően lehet pozitív és negatív is. A távolsággal ellentétben a pont által megtett utat mindig pozitív szám határozza meg. Az út csak akkor esik egybe a távolság abszolút értékével, ha a pont mozgása az origóból indul és egy irányban követi az utat.

A pontmozgás általános esetben az út egyenlő a pont által adott időtartam alatt megtett távolságok abszolút értékeinek összegével:

3. Milyen módokon adható meg egy pont mozgástörvénye?

1. Egy pont mozgásának természetes beállítása.

A mozgás megadásának természetes módszerével feltételezzük, hogy meghatározzuk egy olyan pont mozgásának paramétereit egy mozgó vonatkoztatási rendszerben, amelynek kezdete egybeesik a mozgó ponttal, és a tengelyek az érintő, a normál és a binormális a pont pályája minden pozíciójában. Egy pont mozgási törvényének természetes módon történő beállításához szükséges:

1) ismerje a mozgás pályáját;

2) állítsa be a referenciapontot ezen a görbén;

3) pozitív mozgásirányt kell kialakítani;

4) adja meg egy pont mozgásának törvényét ezen a görbe mentén, azaz! kifejezni az origótól a görbe pontjának adott időpontban elfoglalt helyzetéhez mért távolságot ∪OM=S(t) .

2.Vektoros módszer egy pont mozgásának meghatározására

Ebben az esetben egy pont helyzetét a síkon vagy a térben egy vektorfüggvény határozza meg. Ezt a vektort egy origónak választott fix pontból ábrázoljuk, vége határozza meg a mozgó pont helyzetét.

3. Egy pont mozgásának meghatározására szolgáló koordináta módszer

A kiválasztott koordinátarendszerben a mozgó pont koordinátái az idő függvényében vannak megadva. Egy derékszögű derékszögű koordinátarendszerben ezek az egyenletek:

4. Hogyan irányul a pont valódi sebességének vektora görbe vonalú mozgás során?

Egy pont egyenetlen mozgása esetén sebességének modulusa idővel változik.
Képzeljünk el egy pontot, amelynek mozgását természetes módon az s = f(t) egyenlet adja meg.

Ha a pont rövid Δt ideig megjárta a Δs utat, akkor az átlagos sebessége egyenlő:

vav = ∆s/∆t.

Az átlagsebesség nem ad képet az adott időpillanatban való valódi sebességről (a valódi sebességet egyébként pillanatnyinak nevezik). Nyilvánvaló, hogy minél rövidebb időintervallumra határozzák meg az átlagsebességet, annál közelebb lesz az értéke a pillanatnyi sebességhez.

A valódi (pillanatnyi) sebesség az a határ, amelyre az átlagsebesség hajlik, amikor Δt nullára hajlik:

v = lim v cf t→0-nál vagy v = lim (Δs/Δt) = ds/dt.

Így a valódi sebesség számértéke v = ds/dt.
Egy pont bármely mozgásának valódi (pillanatnyi) sebessége egyenlő a koordináta első deriváltjával (azaz a mozgás kezdőpontjától való távolsággal) az idő függvényében.

Amikor Δt nullára hajlik, Δs is nullára hajlik, és amint azt már megtudtuk, a sebességvektor tangenciálisan lesz irányítva (vagyis egybeesik a v valódi sebességvektorral). Ebből az következik, hogy a v p feltételes sebességvektor határa, amely megegyezik a pont eltolási vektorának egy végtelenül kis időintervallumhoz viszonyított arányának határával, egyenlő a pont valódi sebességvektorával.

5. Hogyan irányul a pont érintő- és normálgyorsulása?

A gyorsulásvektor iránya egybeesik a sebességváltozás irányával Δ = - 0

A tangenciális gyorsulás egy adott pontban érintőlegesen irányul a pont pályájára; ha a mozgás felgyorsult, akkor a tangenciális gyorsulási vektor iránya egybeesik a sebességvektor irányával; ha a mozgás lassú, akkor a tangenciális gyorsulásvektor iránya ellentétes a sebességvektor irányával.

6. Milyen mozgást végez a pont, ha az érintőleges gyorsulás nulla, és a normál nem változik az idő múlásával?

Egyenletes görbe vonalú mozgás azzal jellemezve, hogy a sebesség számértéke állandó ( v= konst), a sebesség csak irányban változik. Ebben az esetben a tangenciális gyorsulás nulla, hiszen v= konst(b. ábra),

és a normál gyorsulás nem egyenlő nullával, hiszen r - végső érték.

7. Hogyan néznek ki a kinematikai gráfok egyenletes és egyformán változó mozgással?

Egyenletes mozgással a test bármely egyenlő időintervallumban egyenlő távolságokat tesz meg. Az egyenletes egyenes vonalú mozgás kinematikai leírásához a koordinátatengely ÖKÖR kényelmesen elhelyezhető a mozgásvonal mentén. A test helyzetét egyenletes mozgás közben egy koordináta beállításával határozzuk meg x. Az elmozdulásvektor és a sebességvektor mindig a koordinátatengellyel párhuzamosan irányul ÖKÖR. Ezért az egyenes vonalú mozgás közbeni elmozdulás és sebesség a tengelyre vetíthető ÖKÖRés vetületeiket tekintsük algebrai mennyiségeknek.

Egyenletes mozgásnál az út lineáris összefüggés szerint változik. koordinátákban. A grafikon egy ferde vonal.

A téma tanulmányozása eredményeként a hallgatónak:

van ötleted térről, időről, pályáról; átlagos és valós sebesség;

tud egy pont mozgásának megadásának módjai; pont mozgásának paraméterei egy adott pálya mentén.

4. előadás. Súlypont.

Ez az előadás a következő kérdéseket fedi le

1. Merev test súlypontja.

2. Inhomogén testek súlypontjainak koordinátái.

3. Homogén testek súlypontjainak koordinátái.

4. A súlypontok koordinátáinak meghatározására szolgáló módszerek.

5. Néhány homogén test súlypontja.

Ezeknek a kérdéseknek a vizsgálata a jövőben szükséges a testek mozgásának dinamikájának tanulmányozásához, figyelembe véve a csúszósúrlódást és a gördülési súrlódást, a mechanikai rendszer tömegközéppontjának mozgásának dinamikáját, a mozgási nyomatékokat, a problémák megoldásához. az "Anyagok szilárdsága" tudományágban.

Párhuzamos erők hozása.

Miután megvizsgáltuk a lapos rendszer középpontjára való redukciót és az erők tetszőleges térbeli rendszerét, ismét visszatérünk a párhuzamos erőrendszer egy konkrét esetére.

Két párhuzamos erőt hozva.

Egy ilyen erőrendszer mérlegelése során a következő három csökkentési eset lehetséges.

1. Két kollineáris erő rendszere. Tekintsünk két párhuzamos és azonos irányú erőből álló rendszert PÉs K pontokon alkalmazva DEÉs BAN BEN. Feltételezzük, hogy az erők merőlegesek erre a szakaszra (1. ábra, de).

TÓL TŐL szegmenshez tartozó ABés megfelel a feltételnek:

AC/SW = K/P.(1)

Fő rendszervektor RC = P + K modulo egyenlő ezen erők összegével: RC = P + K.

TÓL TŐL figyelembe véve (1) egyenlő nullával:MC = P ∙ AC- K∙ SW = 0.

Így a szereposztás eredményeként a következőket kaptuk: RC ≠ 0, MC= 0. Ez azt jelenti, hogy a fővektor ekvivalens a redukciós középponton áthaladó eredővel, azaz:

A kollineáris erők eredője abszolút értékben egyenlő az összegükkel, és hatásvonala felosztja az alkalmazásuk pontjait összekötő szakaszt, fordítottan arányosan ezen erők belső moduljaival.

Vegye figyelembe, hogy a pont helyzete TÓL TŐL nem fog változni, ha az erők RÉs K sarkon fordulniα . Pont TÓL TŐL, amely rendelkezik ezzel a tulajdonsággal, az úgynevezett párhuzamos erők középpontja.

2. Kettős rendszer antikollineárisés nem egyenlő az erőmodulussal. Legyenek az erők PÉs K pontokon alkalmazva DEÉs BAN BEN, párhuzamos, ellentétes irányú és nem egyenlő modulusú (1. ábra, b).

Válasszuk a pontot referencia középpontnak TÓL TŐL, amely továbbra is kielégíti az (1) összefüggést, és ugyanazon az egyenesen fekszik, de a szakaszon kívül AB.

Ennek a rendszernek a fő vektora RC = P + K A modulo most egyenlő lesz a vektorok moduljai közötti különbséggel: RC = K - P.

Fő momentum a központtal kapcsolatban TÓL TŐL még mindig nulla:MC = P ∙ AC- K∙ SW= 0, tehát

Eredő antikollineáris az abszolút értékben nem egyenlő erők pedig egyenlő a különbségükkel, nagyobb erő felé irányulnak, és hatásvonala felosztja az alkalmazási pontjait összekötő szakaszt, fordítottan arányosan ezen erők külső moduljaival.

1. ábra

3. Kettős rendszer antikollineárisés a modulusban egyenlő erők. Vegyük kezdeti esetnek a redukció előző esetét. Tegyük rendbe az áramot R, és erő K törekedjünk a modulo erőltetésre R.

Aztán at K → R az (1) képletben az arány AC/SW → 1. Ez azt jelenti AC → SW, vagyis a távolság AC →∞ .

Ebben az esetben a fővektor modulja RC → 0, és a fő momentum modulja nem függ a redukciós középpont helyzetétől, és egyenlő marad az eredeti értékkel:

MC = P ∙ AC- K∙ SW = P ∙ ( AC- SW) =P ∙ DEB.

Így a határértékben olyan erőrendszert kaptunk, amelyre RC = 0, MC≠ 0, és a redukciós középpont a végtelenségig el lesz távolítva, ami nem helyettesíthető az eredővel. Ebben a rendszerben nem nehéz egy pár erőt kideríteni, tehát egy erőpárnak nincs eredője.

A párhuzamos erők rendszerének középpontja.

Fontolja meg a rendszert n erők Pi pontokon alkalmazvaAi (x i , y i , z i) és párhuzamos a tengellyelOv a vektorral l(2. ábra).

Ha előzetesen kizárjuk egy erőpárral ekvivalens rendszer esetét, akkor nem nehéz az előző bekezdés alapján bizonyítani annak eredőjének létezését.R.

Határozza meg a középpont koordinátáit!C(x c, y c, z c) párhuzamos erők, vagyis ennek a rendszernek az eredője alkalmazási pontjának koordinátái.

Erre a célra a Varignon-tételt használjuk, amely alapján:

M0 (R) = Σ M0(Pi).

2. ábra

Az erő vektor-nyomatéka keresztszorzatként ábrázolható, ezért:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r i× Pi ).

Tekintettel arra R = Rv ∙ l, de Pi = P vi ∙ l és a vektorszorzat tulajdonságait felhasználva kapjuk:

rc × Rv ∙ l = Σ ( r i × P vi ∙ l),

rc ∙ R v × l = Σ ( r i ∙ P vi × l) = Σ ( r i ∙ P vi ) × l,

vagy:

[ r c R v - Σ ( r i P vi )] × l= 0.

Az utolsó kifejezés csak akkor érvényes, ha a szögletes zárójelben lévő kifejezés nulla. Ezért az index elhagyásavés figyelembe véve, hogy az eredőR = Σ Pi , innen kapjuk:

rc = (Σ Pi r i )/(Σ Pi ).

Az utolsó vektoregyenlőséget a koordinátatengelyre vetítve megkapjuk a kívántat párhuzamos erők középpontjának koordinátáinak kifejezése:

x c = (Σ Pi x i)/(Σ Pi );

y c = (Σ Pi y i )/(Σ Pi );(2)

z c = (Σ Pi z i )/(Σ Pi ).

A test súlypontja

Homogén test súlypontjainak koordinátái.

Vegyünk egy merev testsúlyt Pés hangerőt V koordináta-rendszerben Oxyz, ahol a tengelyek xÉs y kapcsolódik a Föld felszínéhez és a tengelyhez z a zenit felé irányítják.

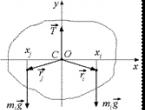
Ha a testet elemi részekre bontjuk egy hangerővel∆ V én , akkor a vonzás ereje hat annak minden részére∆ Pia föld közepe felé irányul. Tegyük fel, hogy a test méretei jóval kisebbek, mint a Föld méretei, akkor a test elemi részeire ható erőrendszer nem konvergálónak, hanem párhuzamosnak tekinthető (3. ábra), és ebből az összes következtetés. az előző fejezetben foglaltak vonatkoznak rá.

3. ábra

Meghatározás . A merev test tömegközéppontja ennek a testnek az elemi részei párhuzamos gravitációs erőinek középpontja.

Emlékezzen arra fajsúly a test elemi részét súlyának arányának nevezzük∆ Pi hangerőhöz ∆ V én : γ én = ∆ Pi/ ∆ V én . Homogén test esetén ez az érték állandó:γ én = γ = P/ V.

Behelyettesítés (2) ∆-be Pi = γ én ∙∆ V én ahelyett Pi, figyelembe véve az utolsó megjegyzést és csökkentve a számlálót és a nevezőtg, kapunk homogén test súlypontjának koordinátáinak kifejezései:

x c = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

y c = (Σ ∆ Vi∙ y i )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Számos tétel hasznos a súlypont meghatározásában.

1) Ha egy homogén testnek van szimmetriasíkja, akkor a súlypontja ebben a síkban van.

Ha a tengelyek xÉs nál nél ebbe a szimmetriasíkba helyezve, majd minden koordinátapontra. és koordinálja (3) szerint nullával egyenlő lesz, mert összesen minden az ellentétes előjelű kifejezések páronként kiesnek. Tehát a súlypont az a szimmetria síkjában.

2) Ha egy homogén testnek van szimmetriatengelye, akkor a test súlypontja ezen a tengelyen található.

Valóban, ebben az esetben, ha a tengelyzrajzoljon a szimmetriatengely mentén, minden pontra koordinátákkalkoordinátákkal találhat egy pontotés koordináták és a (3) képletekkel számolva egyenlő lesz nullával.

A harmadik tétel is hasonlóképpen bizonyított.

3) Ha egy homogén testnek van szimmetriaközéppontja, akkor a test súlypontja ezen a ponton található.

És még néhány megjegyzés.

Első. Ha a test olyan részekre osztható, amelyeknél ismert a súlypont és a súlypont helyzete, akkor nem kell minden pontot figyelembe venni, hanem a (3) képletekben. Pi – az érintett alkatrész súlyaként kell meghatározni ésmint a súlypontjának koordinátái.

Második. Ha a test homogén, akkor annak egy különálló részének súlya, ahol annak az anyagnak a fajsúlya, amelyből a test készült, és Vi - ennek a testrésznek a térfogata. És a (3) képletek kényelmesebb formát öltenek. Például,

És hasonlóképpen hol - az egész test térfogata.

Harmadik megjegyzés. Hagyja, hogy a test úgy nézzen ki, mint egy vékony lemez Fés vastagsága t a repülőben fekve Oxy. Behelyettesítés (3)∆ V én =t ∙ ∆F én , megkapjuk egy homogén lemez súlypontjának koordinátáit:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z én ) / (Σ ∆ F i).

ahol – az egyes lemezek súlypontjának koordinátái;a test teljes területe.

Negyedik megjegyzés. Vékony görbe vonalú rúd alakú testhez, amelynek hossza L keresztmetszeti területtel a elemi kötet∆ V én = a ∙∆ L én , ezért vékony görbe vonalú rúd súlypontjának koordinátái egyenlő lesz:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

ahol – a súlypont koordinátáién-edik szakasz; .

Vegye figyelembe, hogy a definíció szerint a súlypont egy geometriai pont; adott test határain kívül is elhelyezkedhet (például egy gyűrű esetében).

Jegyzet.

A tanfolyam ezen részében nem teszünk különbséget gravitáció, gravitáció és testsúly között. A valóságban a gravitáció a Föld gravitációja és a forgásából eredő centrifugális erő közötti különbség.

Inhomogén testek súlypontjainak koordinátái.

A súlypont koordinátái inhomogén szilárd anyag(4. ábra) a kiválasztott referenciarendszerben a következőképpen határozhatók meg:

4. ábra

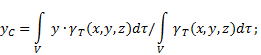
ahol - egységnyi térfogatú tömeg (fajsúly)

- teljes testtömeg.

egyenetlen felület(5. ábra), akkor a kiválasztott vonatkoztatási rendszerben a súlypont koordinátáit a következőképpen határozzuk meg:

5. ábra

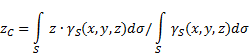
ahol - testfelület egységnyi tömege

- teljes testtömeg.

Ha a szilárd heterogén vonal(6. ábra), akkor a kiválasztott vonatkoztatási rendszerben a súlypont koordinátáit a következőképpen határozzuk meg:

6. ábra

ahol - testhossz egységsúly,

Teljes testtömeg.

A súlypont koordinátáinak meghatározására szolgáló módszerek.

A fent kapott általános képletek alapján lehetőség van konkrét módszerek megjelölésére testek súlypontjainak koordinátáinak meghatározása.

7. ábra

2. Hasítás. A test véges számú részre van osztva (8. ábra), amelyek mindegyikénél ismert a súlypont helyzete és a terület.

8. ábra

S \u003d S 1 + S 2.

3.A negatív területek módszere. A particionálási módszer speciális esete (9. ábra). Kivágással rendelkező testekre vonatkozik, ha a kivágás nélküli test súlypontja és a kivágás ismert. A kivágással ellátott lemez alakú testet egy tömör lemez (kivágás nélkül) kombinációja ábrázolja egy területtel S1 és a kivágott rész területe S2.

9. ábra

S \u003d S 1 - S 2.

Egyes homogén testek súlypontjai.

1) Egy körív súlypontja. Vegye figyelembe az ívet AB sugárR központi szöggel. A szimmetria miatt ennek az ívnek a súlypontja a tengelyen fekszikÖkör(10. ábra).

10. ábra

Keressük a koordinátát képlet szerint . Ehhez válassza ki az íven AB elem MM ’ hosszú, amelynek helyzetét a szög határozza meg. Koordináta x elem MM' akarat. Ezeket az értékeket helyettesítve xÉs d l és szem előtt tartva, hogy az integrált az ív teljes hosszára kell kiterjeszteni, a következőt kapjuk:

ahol L az AB ív hossza egyenlő.

Innentől végre azt találjuk, hogy a körív súlypontja a szimmetriatengelyén van a középponttól távol.Ó egyenlő

hol van a szög radiánban mérve.

2) A háromszög területének súlypontja. Tekintsünk egy háromszöget, amely a síkban fekszik Oxy, melynek csúcskoordinátái ismertek: Ai (x i,y i ), (én= 1,2,3). A háromszög oldalával párhuzamos keskeny csíkokra bontása DE 1 DE 2 , arra a következtetésre jutunk, hogy a háromszög súlypontjának a mediánhoz kell tartoznia DE 3 M 3 (11. ábra) .

11. ábra

Különösen a medián esetében DE 1 M 1-et kapunk, mivel a pont koordinátái M 1 - a csúcsok koordinátáinak számtani átlaga DE 2 és DE 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Így a háromszög súlypontjának koordinátái a csúcsok koordinátáinak számtani átlagai:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

3) A kör alakú szektor területének súlypontja. Tekintsünk egy kör sugarú szektorát R középső szöggel 2α , szimmetrikusan helyezkedik el a tengely körül Ökör (12. ábra) .

Ez nyilvánvaló y c = 0, és a távolság annak a körnek a középpontjától, amelyből ez a szektor el van vágva a súlypontig, a következő képlettel határozható meg:

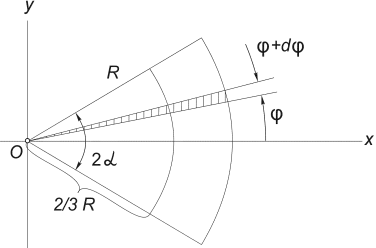
12. ábra

Ezt az integrált a legegyszerűbben úgy számíthatjuk ki, hogy az integrációs tartományt elemi szektorokra osztjuk egy szöggel dφ . Az első rendű végtelen kicsikig egy ilyen szektor helyettesíthető egy háromszöggel, amelynek alapja egyenlő R × dφ és magasság R. Egy ilyen háromszög területe dF =(1/2)R 2 ∙ dφ , súlypontja pedig 2/3 R felülről, így az (5)-be tesszük x = (2/3)R∙ cos. Behelyettesítés (5) F= α R 2, kapjuk:

Az utolsó képlet segítségével kiszámítjuk különösen a súlypont távolságát félkör.

Ha a (2)-ben α = π /2-t helyettesítünk, a következőt kapjuk: x c = (4 R)/(3 π ) ≅ 0,4 R .

1. példaHatározzuk meg az ábrán látható homogén test súlypontját! 13.

13. ábra

Megoldás.A test homogén, két szimmetrikus formájú részből áll. Súlypontjuk koordinátái:

Köteteik:

Ezért a test súlypontjának koordinátái

2. példa Keresse meg a derékszögben meghajlított lemez súlypontját! Méretek - a rajzon (14. ábra).

14. ábra

Megoldás. Súlypont koordináták:

Négyzetek:

Ezért:

3. példa Egy négyzet alakú lapon cm-es vágott négyzet alakú lyukat lásd (15. ábra). Keresse meg a lap súlypontját. 4. példa Határozza meg a lemez súlypontjának helyzetét az ábrán látható módon! 16. A méretek centiméterben vannak megadva.

16. ábra

Megoldás. A lemezt figurákra osztjuk (17. ábra), központok amelynek súlyossága ismert.

Ezen ábrák területei és súlypontjaik koordinátái:

1) egy téglalap 30 és 40 cm-es oldalakkal,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; nál nél 1 \u003d 20 cm.

2) derékszögű háromszög, amelynek alapja 50 cm és magassága 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; x 2 = 30 + 50 / 3 \u003d 46,7 cm; y 2 =40/3 =13,3 cm;

3) félkör kör sugara r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; x 3 =4 R /3 π =8,5 cm; nál nél

Megoldás. Emlékezzünk vissza, hogy a fizikában a test sűrűségeρ és fajsúlyagarányával összefügg:γ = ρ g , aholg - a gravitáció gyorsulása. Egy ilyen homogén test tömegének meghatározásához meg kell szoroznia a sűrűséget a térfogatával.

19. ábra

A "lineáris" vagy "lineáris" sűrűség kifejezés azt jelenti, hogy a rácsos rúd tömegének meghatározásához a lineáris sűrűséget meg kell szorozni a rúd hosszával.

A probléma megoldásához használhatja a particionálási módszert. Ha egy adott rácsot 6 különálló rúd összegeként ábrázolunk, a következőt kapjuk:

aholL i hosszén -th rúd a gazdaság, ésx i , y i - súlypontjának koordinátáit.

Így egy adott rácsos tartó csak két rúdcsoport kombinációjával ábrázolható.

Az első csoport az első rúdból állL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. A második rúdcsoport öt rúdból áll, amelyekhezL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

A gazdaság súlypontjának koordinátáit a következő képlet határozza meg:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Kérdések önvizsgálathoz

Mi a párhuzamos erők középpontja?

- Hogyan határozzák meg a párhuzamos erők középpontjának koordinátáit?

- Hogyan határozható meg a párhuzamos erők középpontja, amelyek eredője nulla?

Mi a tulajdonsága a párhuzamos erők középpontjának?

- Milyen képletekkel számítják ki a párhuzamos erők középpontjának koordinátáit?

Mi a test súlypontja?

- Miért tekinthetők párhuzamos erők rendszerének a Föld vonzási erői, amelyek a test egy pontjára hatnak?

- Írja fel az inhomogén és homogén testek súlypontjának meghatározására szolgáló képletet, a síkszelvények súlypontjának meghatározására szolgáló képletet?

- Írja le az egyszerű geometriai alakzatok súlypontjának meghatározására szolgáló képletet: téglalap, háromszög, trapéz és fél kör?

Mit nevezünk a terület statikus momentumának?

- Mondjon példát olyan testre, amelynek súlypontja a testen kívül található!

- Hogyan használják a szimmetriatulajdonságokat a testek súlypontjainak meghatározására?

- Mi a lényege a negatív súlyozás módszerének?

Hol található a körív súlypontja?

Hogyan találhatja meg grafikusan egy háromszög súlypontját?

- Írja fel a körszektor súlypontját meghatározó képletet!

- A háromszög és egy körszektor súlypontját meghatározó képletek felhasználásával állítsa le a körszakaszhoz hasonló képletet.

- Milyen képletekkel számítják ki a homogén testek, sík alakok és egyenesek súlypontjainak koordinátáit?

- Mit nevezünk egy lapos alakzat területének statikus nyomatékának a tengelyhez képest, hogyan számítják ki és milyen méretei vannak?

- Hogyan határozható meg a terület súlypontjának helyzete, ha ismert az egyes részeinek súlypontjainak helyzete?

- Milyen segédtételeket használunk a súlypont helyzetének meghatározásához?

Rajzolja fel a rendszer diagramját, és jelölje meg rajta a súlypontot. Ha a talált súlypont az objektumrendszeren kívül van, akkor rossz választ kaptál. Lehetséges, hogy különböző referenciapontoktól mért távolságot. Ismételje meg a méréseket.

Például, ha gyerekek ülnek a hintán, a súlypont valahol a gyerekek között lesz, és nem a hintától jobbra vagy balra. Ezenkívül a súlypont soha nem esik egybe azzal a ponttal, ahol a gyermek ül.
Ezek az érvelések helyesek a kétdimenziós térben. Rajzolj egy négyzetet, amely illeszkedik a rendszer összes objektumához. A súlypontnak ezen a négyzeten belül kell lennie.

Ha kis eredményt kap, ellenőrizze a matematikát. Ha az origó a rendszer egyik végén van, a kis eredmény a súlypontot a rendszer végéhez közel helyezi. Lehet, hogy ez a helyes válasz, de az esetek túlnyomó többségében egy ilyen eredmény hibára utal. A pillanatok kiszámításakor megszoroztad a megfelelő súlyokat és távolságokat? Ha a szorzás helyett súlyokat és távolságokat ad hozzá, sokkal kisebb eredményt kap.

Javítsa ki a hibát, ha több súlypontot talál. Minden rendszernek csak egy súlypontja van. Ha több súlypontot talált, valószínűleg nem adta össze az összes pontot. A súlypont egyenlő a "teljes" nyomaték és a "teljes" tömeg arányával. Nem kell "minden" pillanatot elosztani "minden" súllyal: így találja meg az egyes tárgyak helyzetét.

Ellenőrizze a referenciapontot, ha a válasz valamilyen egész értékkel eltér. Példánkban a válasz 3,4 m. Tegyük fel, hogy 0,4 m-es vagy 1,4 m-es választ kapott, vagy más „.4”-re végződő számot. Ennek az az oka, hogy nem a tábla bal oldalát választotta referenciapontnak, hanem egy olyan pontot, amely egész számmal jobbra található. Valójában a válaszod helyes, függetlenül attól, hogy milyen hivatkozási pontot választasz! Ne feledje: a referenciapont mindig az x = 0 pozícióban van. Íme egy példa:

Példánkban a referenciapont a tábla bal oldalán volt, és azt találtuk, hogy a súlypont 3,4 m-re van ettől a referenciaponttól.
Ha olyan pontot választunk referenciapontnak, amely 1 m távolságra van a tábla bal szélétől jobbra, akkor 2,4 m választ kapunk, vagyis a súlypont távolsága kb. 2,4 m-re az új referenciaponttól, amely viszont 1 m-re található a tábla bal végétől. Így a súlypont 2,4 + 1 = 3,4 m távolságra van a tábla bal végétől. Kaptam egy régi választ!
Megjegyzés: Távolságméréskor ne feledje, hogy a "bal" referenciapont távolsága negatív, és a "jobb" referenciapont távolsága pozitív.

Mérje meg a távolságokat egyenes vonalakban. Tegyük fel, hogy két gyerek van egy hintán, de az egyik gyerek sokkal magasabb, mint a másik, vagy az egyik gyerek a deszka alatt lóg, ahelyett, hogy rajta ülne. Hagyja figyelmen kívül ezt a különbséget, és mérje meg a távolságokat a tábla egyenes vonala mentén. A távolságok szögben történő mérése közeli, de nem egészen pontos eredményekhez vezet.

A lengődeszka probléma esetén ne feledje, hogy a súlypont a deszka jobb és bal vége között van. Később megtanulja, hogyan kell kiszámítani a bonyolultabb kétdimenziós rendszerek súlypontját.

szerző: Vegyünk egy tetszőleges alakú testet. Fel lehet-e akasztani egy cérnára úgy, hogy a felakasztás után megtartsa a helyzetét (azaz ne kezdjen el forogni), amikor Bármi kezdeti tájolás (27.1. ábra)?

Más szóval, van-e olyan pont, amelyhez képest a test különböző részein ható gravitációs erők nyomatékainak összege nullával egyenlő lenne Bármi a test orientációja a térben?

Olvasó: Szerintem igen. Az ilyen pontot az ún a test súlypontja.

Bizonyíték. Az egyszerűség kedvéért tekintsünk egy tetszőleges alakú, lapos lemez formájú testet, amely tetszőlegesen van elhelyezve a térben (27.2. ábra). Vegyük a koordináta-rendszert x 0nál nél az origóval a tömegközéppontban - egy pont TÓL TŐL, azután x C = 0, C-nél = 0.

Ezt a testet nagyszámú ponttömeg gyűjteményeként ábrázoljuk m i, amelyek mindegyikének helyzetét a sugárvektor adja meg.

A tömegközéppont és a koordináta meghatározása szerint x C = .

Mivel a koordináta-rendszerünkben x C= 0, akkor . Szorozzuk meg ezt az egyenletet ezzel gés kap

ábrából látható. 27.2, | x i| az erő válla. És ha x i> 0, akkor az erőnyomaték M i> 0, és ha x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i az erő pillanata lesz M i = m i gx i . Ekkor az (1) egyenlőség ekvivalens , ahol M i a gravitációs pillanat. És ez azt jelenti, hogy a test tetszőleges orientációjával a testre ható gravitációs erők momentumainak összege a tömegközépponthoz képest nullával egyenlő.

Ahhoz, hogy az általunk vizsgált test egyensúlyban legyen, egy ponton alkalmazni kell rá TÓL TŐL erő T = mg függőlegesen felfelé mutat. Ennek az erőnek a pillanata a pontról TÓL TŐL egyenlő nullával.

Mivel okfejtésünk nem függött attól, hogy a test pontosan hogyan tájolódik a térben, így bebizonyítottuk, hogy a tömegközéppont egybeesik a tömegközépponttal, amit bizonyítani kellett.

Probléma 27.1. Keresse meg egy súlytalan hosszúságú rúd súlypontját l, melynek végein két ponttömeg van rögzítve T 1 és T 2 .

T 1 T 2 l	Megoldás. Nem a súlypontot fogjuk keresni, hanem a tömegközéppontot (hiszen egy és ugyanaz). Mutassuk be a tengelyt x(27.3. ábra). Rizs. 27.3
x C =?

Válasz: távol a tömegtől T 1 .

ÁLLJON MEG! Döntse el Ön: B1-B3.

1. állítás . Ha egy homogén lapos testnek van szimmetriatengelye, akkor ezen a tengelyen van a súlypont.

Valójában bármilyen ponttömegre m i, amely a szimmetriatengelytől jobbra helyezkedik el, ugyanaz a ponttömeg található szimmetrikusan az elsőhöz képest (27.4. ábra). Ebben az esetben az erőnyomatékok összege .

Mivel az egész testet hasonló pontpárokra bontva ábrázolhatjuk, a szimmetriatengelyen elhelyezkedő bármely ponthoz viszonyított összsúlynyomaték nulla, ami azt jelenti, hogy a test súlypontja is ezen a tengelyen található. Ez egy fontos következtetéshez vezet: ha a testnek több szimmetriatengelye van, akkor a súlypont ezeknek a tengelyeknek a metszéspontjában van(27.5. ábra).

Rizs. 27.5

2. állítás. Ha két test tömegével T 1 és T A 2. ábrán látható testek tömegközéppontja az első és a második test tömegközéppontját összekötő egyenes vonalon helyezkedik el (27.6. ábra).

Rizs. 27.6 Rizs. 27.7

Bizonyíték. Rendezzük el az összetett testet úgy, hogy a testek súlypontjait összekötő szakasz függőleges legyen. Ekkor az első test gravitációs nyomatékainak összege a ponthoz képest TÓL TŐL 1 egyenlő nullával, és a pont körüli második test gravitációs nyomatékainak összege TÓL TŐL 2 nulla (27.7. ábra).

vegye észre, az váll bármely ponttömeg gravitációja t i ugyanaz a szakasz bármely pontjára vonatkozóan TÓL TŐL 1 TÓL TŐL 2 , és ebből adódóan a gravitációs nyomaték a szakasz bármely pontjához viszonyítva TÓL TŐL 1 TÓL TŐL 2 ugyanaz. Ezért az egész test gravitációja nulla a szakasz bármely pontjához képest TÓL TŐL 1 TÓL TŐL 2. Így az összetett test súlypontja a szegmensen fekszik TÓL TŐL 1 TÓL TŐL 2 .

A 2. állítás egy fontos gyakorlati következtetést von maga után, amely egyértelműen utasítások formájában van megfogalmazva.

utasítás,

hogyan lehet megtalálni egy merev test súlypontját, ha törhető

részekre, amelyek mindegyikének a súlypontjainak helyzete ismert

1. Cserélje ki az egyes alkatrészeket az adott alkatrész súlypontjában található tömeggel.

2. Keresse meg gravitáció középpontja(és ez megegyezik a súlyponttal) a kapott tömegpontrendszerből, egy kényelmes koordináta-rendszer kiválasztásával x 0nál nél, a képletek szerint:

Valóban, helyezzük el az összetett testet úgy, hogy a szegmens TÓL TŐL 1 TÓL TŐL 2 vízszintes volt, és pontokon felakasztjuk szálakra TÓL TŐL 1 és TÓL TŐL 2 (27.8. ábra, de). Nyilvánvaló, hogy a test egyensúlyban lesz. És ez az egyensúly nem fog felborulni, ha minden testet ponttömegekkel helyettesítünk T 1 és T 2 (27.8. ábra, b).

Rizs. 27.8

ÁLLJON MEG! Döntse el Ön: C3.

27.2 probléma. Tömeggolyókat helyezünk egy egyenlő oldalú háromszög két csúcsára T minden. A harmadik csúcs egy 2 tömegű golyót tartalmaz T(27.9. ábra, de). Háromszög oldal de. Határozza meg ennek a rendszernek a súlypontját.

T 2T de	Rizs. 27.9
x C = ? C-nél = ?

Megoldás. Bemutatjuk a koordinátarendszert x 0nál nél(27.9. ábra, b). Azután

Válasz: x C = de/2; ; a súlypont a magasság felében van HIRDETÉS.