szerző: Vegyünk egy tetszőleges alakú testet. Fel lehet-e akasztani egy cérnára úgy, hogy a felakasztás után megtartsa a helyzetét (azaz ne kezdjen el forogni), amikor Bármi kezdeti tájolás (27.1. ábra)?

Más szóval, van-e olyan pont, amelyhez képest a test különböző részein ható gravitációs erők nyomatékainak összege nullával egyenlő lenne Bármi a test orientációja a térben?

Olvasó: Szerintem igen. Az ilyen pontot az ún a test súlypontja.

Bizonyíték. Az egyszerűség kedvéért tekintsünk egy tetszőleges alakú, lapos lemez formájú testet, amely tetszőlegesen van elhelyezve a térben (27.2. ábra). Vegyük a koordináta-rendszert x 0nál nél az origóval a tömegközéppontban - egy pont TÓL TŐL, azután x C = 0, C-nél = 0.

Ezt a testet nagyszámú ponttömeg gyűjteményeként ábrázoljuk m i, amelyek mindegyikének helyzetét a sugárvektor adja meg.

A tömegközéppont és a koordináta meghatározása szerint x C = .

Mivel a koordináta-rendszerünkben x C= 0, akkor . Szorozzuk meg ezt az egyenletet ezzel gés kap

ábrából látható. 27.2, | x i| az erő válla. És ha x i> 0, akkor az erőnyomaték M i> 0, és ha x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i az erő pillanata lesz M i = m i gx i . Ekkor az (1) egyenlőség ekvivalens , ahol M i a gravitációs pillanat. És ez azt jelenti, hogy a test tetszőleges orientációjával a testre ható gravitációs erők momentumainak összege a tömegközépponthoz képest nullával egyenlő.

Ahhoz, hogy az általunk vizsgált test egyensúlyban legyen, egy ponton alkalmazni kell rá TÓL TŐL Kényszerítés T = mg függőlegesen felfelé mutat. Ennek az erőnek a pillanata a pontról TÓL TŐL egyenlő nullával.

Mivel okfejtésünk nem függött attól, hogy a test pontosan hogyan tájolódik a térben, így bebizonyítottuk, hogy a tömegközéppont egybeesik a tömegközépponttal, amit bizonyítani kellett.

Probléma 27.1. Keresse meg egy súlytalan hosszúságú rúd súlypontját l, melynek végein két ponttömeg van rögzítve T 1 és T 2 .

T 1 T 2 l	Megoldás. Nem a súlypontot fogjuk keresni, hanem a tömegközéppontot (hiszen egy és ugyanaz). Mutassuk be a tengelyt x(27.3. ábra). Rizs. 27.3
x C =?

Válasz: távol a tömegtől T 1 .

ÁLLJON MEG! Döntse el Ön: B1-B3.

1. állítás . Ha egy homogén lapos testnek van szimmetriatengelye, akkor ezen a tengelyen van a súlypont.

Valójában bármilyen ponttömegre m i, amely a szimmetriatengelytől jobbra helyezkedik el, ugyanaz a ponttömeg található szimmetrikusan az elsőhöz képest (27.4. ábra). Ebben az esetben az erőnyomatékok összege .

Mivel az egész testet hasonló pontpárokra bontva ábrázolhatjuk, a szimmetriatengelyen elhelyezkedő bármely ponthoz viszonyított összsúlynyomaték nulla, ami azt jelenti, hogy a test súlypontja is ezen a tengelyen található. Ez egy fontos következtetéshez vezet: ha a testnek több szimmetriatengelye van, akkor a súlypont ezeknek a tengelyeknek a metszéspontjában van(27.5. ábra).

Rizs. 27.5

2. állítás. Ha két test tömegével T 1 és T A 2. ábrán látható testek tömegközéppontja az első és a második test tömegközéppontját összekötő egyenes vonalon helyezkedik el (27.6. ábra).

Rizs. 27.6 Rizs. 27.7

Bizonyíték. Rendezzük el az összetett testet úgy, hogy a testek súlypontjait összekötő szakasz függőleges legyen. Ekkor az első test gravitációs nyomatékainak összege a ponthoz képest TÓL TŐL 1 egyenlő nullával, és a pont körüli második test gravitációs nyomatékainak összege TÓL TŐL 2 nulla (27.7. ábra).

vegye észre, az váll bármely ponttömeg gravitációja t i ugyanaz a szakasz bármely pontjára vonatkozóan TÓL TŐL 1 TÓL TŐL 2 , és ebből adódóan a gravitációs nyomaték a szakasz bármely pontjához viszonyítva TÓL TŐL 1 TÓL TŐL 2 ugyanaz. Ezért az egész test gravitációja nulla a szakasz bármely pontjához képest TÓL TŐL 1 TÓL TŐL 2. Így az összetett test súlypontja a szegmensen fekszik TÓL TŐL 1 TÓL TŐL 2 .

A 2. állítás egy fontos gyakorlati következtetést von maga után, amely egyértelműen utasítások formájában van megfogalmazva.

utasítás,

hogyan lehet megtalálni egy merev test súlypontját, ha törhető

részekre, amelyek mindegyikének a súlypontjainak helyzete ismert

1. Cserélje ki az egyes alkatrészeket az adott alkatrész súlypontjában található tömeggel.

2. Keresse meg gravitáció középpontja(és ez megegyezik a súlyponttal) a kapott tömegpontrendszerből, egy kényelmes koordináta-rendszer kiválasztásával x 0nál nél, a képletek szerint:

Valóban, helyezzük el az összetett testet úgy, hogy a szegmens TÓL TŐL 1 TÓL TŐL 2 vízszintes volt, és pontokon felakasztjuk szálakra TÓL TŐL 1 és TÓL TŐL 2 (27.8. ábra, de). Nyilvánvaló, hogy a test egyensúlyban lesz. És ez az egyensúly nem fog felborulni, ha minden testet ponttömegekkel helyettesítünk T 1 és T 2 (27.8. ábra, b).

Rizs. 27.8

ÁLLJON MEG! Döntse el Ön: C3.

27.2 probléma. Tömeggolyókat helyezünk egy egyenlő oldalú háromszög két csúcsára T minden. A harmadik csúcs egy 2 tömegű golyót tartalmaz T(27.9. ábra, de). Háromszög oldal de. Határozza meg ennek a rendszernek a súlypontját.

T 2T de	Rizs. 27.9
x C = ? C-nél = ?

Megoldás. Bemutatjuk a koordinátarendszert x 0nál nél(27.9. ábra, b). Azután

,

.

Válasz: x C = de/2; ; a súlypont a magasság felében van HIRDETÉS.

6.1. Általános információ

Párhuzamos Erők Központja
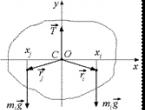
Tekintsünk két párhuzamos erőt, amelyek ugyanabba az irányba irányulnak , és , amelyek a testre a pontokban érvényesülnek DE 1 és DE 2 (6.1. ábra). Ennek az erőrendszernek van egy eredője, amelynek hatásvonala egy bizonyos ponton halad át TÓL TŐL. Pont pozíció TÓL TŐL a Varignon-tétel segítségével találhatjuk meg:

Ha megfordítja az erőt és közel a pontokhoz DE 1 és DE 2 egy irányban és ugyanabban a szögben, akkor egy új párhuzamos zsírrendszert kapunk azonos modulokkal. Ebben az esetben az eredőjük is átmegy a ponton TÓL TŐL. Az ilyen pontot párhuzamos erők középpontjának nevezzük.
Tekintsünk egy merev testre pontokban ható párhuzamos és egyenlő irányú erők rendszerét. Ennek a rendszernek van eredménye.
Ha a rendszer minden egyes erejét az alkalmazási pontok közelében ugyanabban az irányban és azonos szögben elforgatjuk, akkor új, azonos irányú, párhuzamos erőkből álló rendszereket kapunk, azonos modulokkal és alkalmazási pontokkal. Az ilyen rendszerek eredője ugyanazzal a modulussal rendelkezik R, de minden alkalommal más irányba. Lerakott erőt F 1 és F 2 találja meg, hogy az eredőjük R 1 , amely mindig átmegy a ponton TÓL TŐL 1, amelynek helyzetét az egyenlőség határozza meg. Tovább hozzátéve R 1 és F 3 , keresse meg az eredőjüket, amely mindig átmegy a ponton TÓL TŐL 2 a vonalon fekve DE 3 TÓL TŐL 2. Miután az erők összeadásának folyamatát befejeztük, arra a következtetésre jutunk, hogy az összes erő eredője valóban mindig ugyanazon a ponton megy át TÓL TŐL, amelynek a pontokhoz viszonyított helyzete változatlan marad.
Pont TÓL TŐL, amelyen a párhuzamos erők eredő rendszerének hatásvonala áthalad ezen erők alkalmazási pontjai közelében, azonos szögben, azonos irányban, párhuzamos erők középpontjának nevezzük (6.2. ábra).

6.2. ábra

Határozzuk meg a párhuzamos erők középpontjának koordinátáit. A pont helyzete óta TÓL TŐL a testhez képest változatlan, akkor a koordinátái nem függnek a koordinátarendszer megválasztásától. Forgassa el az összes erőt az alkalmazásuk közelében, hogy párhuzamosak legyenek a tengellyel OUés alkalmazzuk a Varignon-tételt elforgatott erőkre. Mivel R" ezeknek az erőknek az eredője, akkor a Varignon-tétel szerint megvan , mivel , , kapunk

Innen megtaláljuk a párhuzamos erők középpontjának koordinátáját zc:

A koordináta meghatározásához xcállítson össze egy kifejezést a tengely körüli erők nyomatékára Oz.

A koordináta meghatározásához yc forgassa el az összes erőt úgy, hogy párhuzamosak legyenek a tengellyel Oz.

A párhuzamos erők középpontjának helyzete az origóhoz képest (6.2. ábra) a sugárvektorával határozható meg:

6.2. Merev test súlypontja

gravitáció középpontja egy merev test egy pontja mindig ehhez a testhez kapcsolódik TÓL TŐL, amelyen áthalad egy adott test gravitációs erői eredőjének hatásvonala, a test tetszőleges térbeli helyzetére.
A súlypontot a testek és a folytonos közegek egyensúlyi helyzetének stabilitásának tanulmányozására használják a gravitáció hatására, és néhány más esetben, nevezetesen: az anyagok ellenállásában és a szerkezeti mechanikában - a Vereshchagin-szabály alkalmazásakor.
A test súlypontjának meghatározásának két módja van: analitikus és kísérleti. A súlypont meghatározásának analitikai módszere közvetlenül a párhuzamos erők középpontjának fogalmából következik.
A súlypont koordinátáit, mint a párhuzamos erők középpontját, a következő képletek határozzák meg:

ahol R- az egész test súlya; pk- a testrészecskék tömege; xk , yk , zk- testrészecskék koordinátái.
Homogén test esetén az egész test és bármely részének súlya arányos a térfogattal P=Vγ, pk =vk γ, ahol γ - egységnyi térfogatú tömeg, V- a test térfogata. Kifejezések helyettesítése P, pk a súlypont koordinátáit meghatározó képletekbe és közös tényezővel redukálva γ , kapunk:

Pont TÓL TŐL, melynek koordinátáit a kapott képletek határozzák meg, nevezzük a kötet súlypontja.
Ha a test vékony, homogén lemez, akkor a súlypontot a következő képletek határozzák meg:

ahol S- a teljes lemez területe; sk- részének területe; xk, yk- a lemezrészek súlypontjának koordinátái.
Pont TÓL TŐL ebben az esetben az ún súlyponti terület.
A síkidomok súlypontjának koordinátáit meghatározó kifejezések számlálóit -val hívjuk a terület statikus pillanatai a tengelyekről nál nélÉs x:

Ezután a terület súlypontja a következő képletekkel határozható meg:

Azon testeknél, amelyek hossza többszöröse a keresztmetszet méreteinek, a vonal súlypontját kell meghatározni. Az egyenes súlypontjának koordinátáit a következő képletek határozzák meg:

ahol L- vonal hossza; lk- részeinek hossza; xk , yk , zk- a vonalrészek súlypontjának koordinátája.

6.3. A testek súlypontjainak koordinátáinak meghatározására szolgáló módszerek

A kapott képletek alapján gyakorlati módszereket lehet javasolni a testek súlypontjainak meghatározására.
1. Szimmetria. Ha a testnek van szimmetriaközéppontja, akkor a súlypont a szimmetria középpontjában van.
Ha a testnek van szimmetriasíkja. Például az XOU sík, akkor a súlypont ebben a síkban található.
2. hasítás. Egyszerű testekből álló testeknél a hasítási módszert alkalmazzuk. A test részekre oszlik, amelyek súlypontját a szimmetria módszerével találjuk meg. Az egész test súlypontját a térfogat (terület) súlypontjának képletei határozzák meg.

Példa. Határozza meg az alábbi ábrán látható lemez súlypontját (6.3. ábra). A lemez többféleképpen osztható téglalapokra, és meghatározható az egyes téglalapok súlypontjának koordinátái és területük.

6.3. ábra

Válasz: xc=17,0 cm; yc= 18,0 cm.

3. Kiegészítés. Ez a módszer a particionálási módszer speciális esete. Akkor használatos, ha a testen vannak bevágások, bevágások stb., ha ismertek a bevágás nélküli test súlypontjának koordinátái.

Példa. Határozza meg egy kör alakú lemez súlypontját, amelynek sugara van kivágással r = 0,6 R(6.4. ábra).

6.4

A kerek lapon szimmetriaközéppont található. Helyezzük a koordináták origóját a lemez közepére. Lemezterület bevágás nélkül, bevágás terület. Fogazott lemezfelület ; .
A hornyolt lemeznek van egy szimmetriatengelye O1 x, Következésképpen yc=0.

4. Integráció. Ha a testet nem lehet véges számú részre osztani, amelyek tömegközéppontjainak helyzete ismert, akkor a testet tetszőleges kis térfogatokra osztjuk, amelyekre a felosztási módszerrel a képlet a következőt kapja: .
Továbbá átmennek a határig, az elemi térfogatokat nullára fordítják, azaz. mennyiségek pontokba bontása. Az összegeket a test teljes térfogatára kiterjesztett integrálok helyettesítik, majd a térfogat súlypontjának koordinátáinak meghatározására szolgáló képletek a következő alakot öltik:

Képletek a terület súlypontjának koordinátáinak meghatározásához:

A lemezek egyensúlyának vizsgálatakor, a szerkezetmechanikai Mohr-integrál számításakor meg kell határozni a terület súlypontjának koordinátáit.

Példa. Határozzuk meg egy sugarú körív súlypontját! R központi szöggel AOB= 2α (6.5. ábra).

Rizs. 6.5

A kör íve szimmetrikus a tengelyre Ó, ezért az ív súlypontja a tengelyen fekszik Ó, yс = 0.
Az egyenes súlypontjának képlete szerint:

6.Kísérleti mód. Az összetett konfigurációjú inhomogén testek súlypontja kísérletileg meghatározható: függesztéssel és mérlegeléssel. Az első mód az, hogy a testet különböző pontokon egy kábelre függesztik fel. A kötél iránya, amelyen a test fel van függesztve, megadja a gravitáció irányát. Ezen irányok metszéspontja határozza meg a test súlypontját.
A mérési módszer abból áll, hogy először meg kell határozni egy test, például egy autó tömegét. Ezután a mérlegen meghatározzák az autó hátsó tengelyének nyomását a tartóra. Egy egyensúlyi egyenlet összeállításával egy bizonyos pontra, például az első kerekek tengelyére vonatkozóan, kiszámíthatja a távolságot ettől a tengelytől az autó súlypontjához (6.6. ábra).

6.6

Néha a problémák megoldása során egyidejűleg különböző módszereket kell alkalmazni a súlypont koordinátáinak meghatározására.

6.4. Néhány egyszerű geometriai alakzat súlypontja

A közös alakú testek (háromszög, körív, szektor, szakasz) súlypontjának meghatározásához célszerű referenciaadatokat használni (6.1. táblázat).

6.1. táblázat

Néhány homogén test súlypontjának koordinátái

№	Az ábra neve	Kép
	körív: egy homogén kör ívének súlypontja a szimmetriatengelyen van (koordináta yc=0). R a kör sugara.
	Homogén körkörös szektor yc=0). ahol α a középponti szög fele; R a kör sugara.
	Szegmens: a súlypont a szimmetriatengelyen helyezkedik el (koordináta yc=0). ahol α a középponti szög fele; R a kör sugara.
	Félkör:
	Háromszög: egy homogén háromszög súlypontja a mediánjainak metszéspontjában van. ahol x1, y1, x2, y2, x3, y3- a háromszög csúcsainak koordinátái
	Kúp: egy homogén körkúp súlypontja a magasságában van, és a magasság 1/4-ére van a kúp alapjától.

Tankönyv 7. évfolyamnak

§ 25.3. Hogyan lehet megtalálni a test súlypontját?

Emlékezzünk vissza, hogy a súlypont a gravitáció alkalmazási pontja. Nézzük meg, hogyan találhatjuk meg kísérletileg egy lapos test súlypontjának helyzetét – mondjuk egy kartonból kivágott tetszőleges alakú alaknál (lásd 12. sz. laboratóriumi munka).

A kartonfigurát tűvel vagy szöggel felakasztjuk, hogy az O ponton átmenő vízszintes tengely körül szabadon foroghasson (25.4. ábra, a). Akkor ez a szám egy O támaszpontú karnak tekinthető.

Rizs. 25.4. Hogyan találjuk meg kísérletileg egy lapos alak súlypontját

Ha egy alak egyensúlyban van, a rá ható erők kiegyenlítik egymást. Ez a T ábra súlypontjában kifejtett F t gravitációs erő és az O pontban kifejtett F rugalmas erőszabályozás (ezt az erőt a csap vagy szög oldaláról fejtik ki).

Ez a két erő csak akkor egyensúlyozza ki egymást, ha ezen erők hatópontjai (T és O pontok) ugyanazon a függőlegesen helyezkednek el (lásd 25.4. ábra, a). Ellenkező esetben a gravitáció elforgatja az ábrát az O pont körül (25.4. ábra, b).

Tehát amikor az ábra egyensúlyban van, a súlypont ugyanazon a függőlegesen helyezkedik el, mint az O felfüggesztési pont. Ez lehetővé teszi az ábra súlypontjának helyzetének meghatározását. Egy függővonallal rajzoljunk egy függőleges vonalat, amely áthalad a felfüggesztési ponton (kék vonal a 25.4. ábrán c). A test súlypontja a megrajzolt vonalon fekszik. Ezt a kísérletet megismételjük a felfüggesztési pont eltérő helyzetével. Ennek eredményeként egy második vonalat kapunk, amelyen a test súlypontja fekszik (zöld vonal a 25.4. ábrán, d). Következésképpen ezen vonalak metszéspontjában van a test kívánt súlypontja (a 25.4. ábrán a G piros pont, d).

A fent kapott általános képletek alapján lehetőség van konkrét módszerek megjelölésére a testek súlypontjainak koordinátáinak meghatározására.

1. Szimmetria. Ha egy homogén testnek van síkja, tengelye vagy szimmetriaközéppontja (7. ábra), akkor a súlypontja a szimmetriasíkban, a szimmetriatengelyben vagy a szimmetriaközéppontban van.

7. ábra

2. Hasítás. A test véges számú részre van osztva (8. ábra), amelyek mindegyikénél ismert a súlypont helyzete és a terület.

8. ábra

3.A negatív területek módszere. A particionálási módszer speciális esete (9. ábra). Kivágással rendelkező testekre vonatkozik, ha a kivágás és a kivágás nélküli test súlypontja ismert. A kivágott lemez formájú testet egy tömör lemez (kivágás nélkül) kombinációja képviseli, amelynek területe S 1 és a kivágott rész S 2 területe.

9. ábra

4.csoportosítási módszer. Jó kiegészítője az utolsó két módszernek. Az ábra alkotóelemeire bontása után kényelmes lehet néhányat újra kombinálni, hogy azután e csoport szimmetriájának figyelembevételével leegyszerűsítsük a megoldást.

Egyes homogén testek súlypontjai.

1) Egy körív súlypontja. Vegye figyelembe az ívet AB sugár R központi szöggel. A szimmetria miatt ennek az ívnek a súlypontja a tengelyen fekszik Ökör(10. ábra).

10. ábra

Keressük meg a koordinátát a képlet segítségével. Ehhez válassza ki az íven AB elem MM' hossza , amelynek helyzetét a szög határozza meg . Koordináta x elem MM' fog . Ezeket az értékeket helyettesítve xés d lés szem előtt tartva, hogy az integrált az ív teljes hosszában ki kell terjeszteni, a következőt kapjuk:

ahol L- ívhossz AB, egyenlő .

Innentől végre azt találjuk, hogy a körív súlypontja a szimmetriatengelyén van a középponttól távol. RÓL RŐL egyenlő

ahol a szöget radiánban mérjük.

2) A háromszög területének súlypontja. Tekintsünk egy háromszöget, amely a síkban fekszik Oxy, melynek csúcskoordinátái ismertek: A i(x i,y i), (én= 1,2,3). A háromszög oldalával párhuzamos keskeny csíkokra bontása DE 1 DE 2 , arra a következtetésre jutunk, hogy a háromszög súlypontjának a mediánhoz kell tartoznia DE 3 M 3 (11. ábra) .

11. ábra

A háromszög oldalával párhuzamos csíkokra bontása DE 2 DE 3 , akkor biztos lehet benne, hogy a mediánon kell feküdnie DE 1 M egy . Ily módon a háromszög súlypontja a mediánjainak metszéspontjában van, amely, mint tudod, elválasztja a harmadik részt minden mediántól, a megfelelő oldaltól számítva.

Különösen a medián esetében DE 1 M 1-et kapunk, mivel a pont koordinátái M 1 a csúcskoordináták számtani átlaga DE 2 és DE 3:

x c = x 1 + (2/3)∙(x M 1 - x 1) = x 1 + (2/3)∙[(x 2 + x 3)/2-x 1 ] = (x 1 +x 2 +x 3)/3.

Így a háromszög súlypontjának koordinátái a csúcsok koordinátáinak számtani átlagai:

x c =(1/3)Σ x i ; y c =(1/3)Σ y i.

3) A kör alakú szektor területének súlypontja. Tekintsünk egy kör sugarú szektorát R 2α középponti szöggel, a tengely körül szimmetrikusan helyezkedik el Ökör(12. ábra) .

Ez nyilvánvaló y c = 0, és a távolság annak a körnek a középpontjától, amelyből ez a szektor el van vágva a súlypontig, a következő képlettel határozható meg:

12. ábra

Ezt az integrált a legegyszerűbben úgy számíthatjuk ki, hogy az integrációs tartományt elemi szektorokra osztjuk egy szöggel dφ. Az első rendű végtelen kicsikig egy ilyen szektor helyettesíthető egy háromszöggel, amelynek alapja egyenlő R× dφ és magasság R. Egy ilyen háromszög területe dF=(1/2)R 2 ∙dφ, súlypontja pedig 2/3 távolságra van R felülről, így az (5)-be tesszük x = (2/3)R∙cosφ. Behelyettesítés (5) F= α R 2, kapjuk:

Az utolsó képlet segítségével kiszámítjuk különösen a súlypont távolságát félkör.

A (2)-ben α = π/2 behelyettesítve kapjuk: x c = (4R)/(3π) ≅ 0,4 R .

1. példa Határozzuk meg az ábrán látható homogén test súlypontját! 13.

13. ábra

A test homogén, két szimmetrikus formájú részből áll. Súlypontjuk koordinátái:

Köteteik:

Ezért a test súlypontjának koordinátái

2. példa Keresse meg a derékszögben meghajlított lemez súlypontját! Méretek - a rajzon (14. ábra).

14. ábra

Súlypont koordináták:

Négyzetek:

Rizs. 6.5.

3. példa Négyzet alakú lapból cm négyzet alakú lyukat vágunk ki (15. ábra). Keresse meg a lap súlypontját.

15. ábra

Ebben a problémában kényelmesebb a testet két részre osztani: egy nagy négyzetre és egy négyzet alakú lyukra. Csak a lyuk területét kell negatívnak tekinteni. Ezután a lap súlypontjának koordinátái a furattal:

koordináta mivel a testnek van szimmetriatengelye (átlója).

4. példa A huzaltartó (16. ábra) három azonos hosszúságú részből áll l.

16. ábra

A szakaszok súlypontjainak koordinátái:

Ezért a teljes konzol súlypontjának koordinátái:

5. példa Határozzuk meg a rácsozat súlypontjának helyzetét, amelynek minden rúdja azonos lineáris sűrűségű (17. ábra).

Emlékezzünk vissza, hogy a fizikában egy test ρ sűrűsége és g fajsúlya a következő összefüggéssel függ össze: γ= ρ g, ahol g- a gravitáció gyorsulása. Egy ilyen homogén test tömegének meghatározásához meg kell szoroznia a sűrűséget a térfogatával.

17. ábra

A "lineáris" vagy "lineáris" sűrűség kifejezés azt jelenti, hogy a rácsos rúd tömegének meghatározásához a lineáris sűrűséget meg kell szorozni a rúd hosszával.

A probléma megoldásához használhatja a particionálási módszert. Ha egy adott rácsot 6 különálló rúd összegeként ábrázolunk, a következőt kapjuk:

ahol L i hossz én-th rúd a gazdaság, és x i, y i súlypontjának koordinátái.

A probléma megoldása leegyszerűsíthető az utolsó 5 rácsos rudak csoportosításával. Könnyen belátható, hogy a negyedik rúd közepén elhelyezkedő szimmetriaközéppontú figurát alkotnak, ahol ennek a rúdcsoportnak a súlypontja található.

Így egy adott rácsos tartó csak két rúdcsoport kombinációjával ábrázolható.

Az első csoport az első rúdból áll L 1 = 4 m, x 1 = 0 m, y 1 = 2 m. A második rúdcsoport öt rúdból áll, amelyekhez L 2 = 20 m, x 2 = 3 m, y 2 = 2 m.

A gazdaság súlypontjának koordinátáit a következő képlet határozza meg:

x c = (L 1 ∙x 1 +L 2 ∙x 2)/(L 1 + L 2) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙y 1 +L 2 ∙y 2)/(L 1 + L 2) = (4,2 + 20,2)/24 = 2 m.

Vegye figyelembe, hogy a központ TÓL TŐL az összekötő vonalon fekszik TÓL TŐL 1 és TÓL TŐL 2, és felosztja a szakaszt TÓL TŐL 1 TÓL TŐL 2 kapcsolatban: TÓL TŐL 1 TÓL TŐL/SS 2 = (x c - x 1)/(x 2 - x c ) = L 2 /L 1 = 2,5/0,5.

Kérdések önvizsgálathoz

Mi a párhuzamos erők középpontja?

Hogyan határozzák meg a párhuzamos erők középpontjának koordinátáit?

Hogyan határozható meg a párhuzamos erők középpontja, amelyek eredője nulla?

Mi a tulajdonsága a párhuzamos erők középpontjának?

Milyen képletekkel számítjuk ki a párhuzamos erők középpontjának koordinátáit?

Mi a test súlypontja?

Miért tekinthetők párhuzamos erők rendszerének a Föld vonzási erői, amelyek a test egy pontjára hatnak?

Írja fel az inhomogén és homogén testek súlypontjának meghatározására szolgáló képletet, a síkszelvények súlypontjának meghatározására szolgáló képletet?

Írja fel az egyszerű geometriai alakzatok súlypontjának meghatározására szolgáló képletet: téglalap, háromszög, trapéz és fél kör?

Mit nevezünk a terület statikus momentumának?

Mondjon példát olyan testre, amelynek súlypontja a testen kívül található!

Hogyan használják a szimmetriatulajdonságokat a testek súlypontjának meghatározására?

Mi a negatív súlyozás módszerének lényege?

Hol található a körív súlypontja?

Milyen grafikus konstrukcióval lehet megkeresni a háromszög súlypontját?

Írja fel a képletet, amely meghatározza egy körszektor súlypontját!

A háromszög és egy körszektor súlypontját meghatározó képletek segítségével állítson elő hasonló képletet egy körszakaszra.

Milyen képletekkel számítják ki a homogén testek, síkidomok és egyenesek súlypontjainak koordinátáit?

Mit nevezünk egy lapos alakzat területének tengelyhez viszonyított statikus nyomatékának, hogyan számítják ki és milyen méretei vannak?

Hogyan határozható meg a terület súlypontjának helyzete, ha ismert az egyes részei súlypontjainak helyzete?

Milyen segédtételeket használnak a súlypont helyzetének meghatározására?

A hatékony meditációhoz, jógához, csikunghoz és hastánchoz is nagyon fontos az egyensúlyban tartás képessége minden erőfeszítés nélkül. Ez az első követelmény, amellyel az ilyen típusú tevékenységekben kezdők szembesülnek, és az egyik oka annak, hogy oktató nélkül nehéz megtenni az első lépéseket. Egy kérdés, amely azt sugallja, hogy egy személy nem ismeri a súlypontját, kissé másképp nézhet ki. Például a qigongban az ember megkérdezi, hogyan lehet ellazulni, és még mindig állva végez mozdulatokat, egy kezdő keleti táncos nem érti, hogyan kell szétválasztani és összehangolni az alsó és felső testrészek mozgásait, és mindkét esetben az emberek túlfeszülnek, és gyakran elveszítik egyensúlyukat. Mozgásuk bizonytalan, esetlen lesz.

Ezért fontos megérteni, hogyan találja meg saját maga a súlypontját, ehhez szellemi munkára és ügyességre is szükség van, de idővel a készség ösztönös szintre kerül.

Mit kell tenni, hogy ne feszítse meg az izmokat, és ugyanakkor ne használjon külső támasztékokat. A válasz kézenfekvő, a támaszt befelé kell mozgatni. Pontosabban, támaszkodjon egy feltételes belső tengelyre. Hová megy ez a tengely? A súlypont fogalma feltételes, de ennek ellenére a fizikában használják. Ott szokás az eredő gravitációs erők alkalmazási pontjaként definiálni. Az eredő gravitációs erő az összes gravitációs erő összessége, figyelembe véve azok hatásának irányát.

Eddig nehéz? Készítsen türelmet.

Vagyis olyan pontot keresünk a testünkben, amely lehetővé teszi, hogy ne essünk el, anélkül, hogy tudatosan harcolnánk a gravitációval. Ez azt jelenti, hogy a föld gravitációját úgy kell irányítani, hogy az a többi ható erővel valahol testünk közepén konvergáljon.

Az ilyen erőirány a testünk kellős közepén egy feltételes tengelyt, egy függőleges felületet hoz létre, ez a súlypont függőlegese. A testnek az a része, amelyen a talajnak támaszkodunk, a lábnyomunk (a lábunkkal a talajnak támaszkodunk). Azon a helyen, ahol ez a függőleges rátámaszkodik arra a felületre, amelyen állunk, vagyis a talajnak támaszkodunk, ez a súlypont a lábnyomon belül. Ha a függőleges eltolódik erről a helyről, elveszítjük egyensúlyunkat és esünk. Minél nagyobb maga a támasztófelület, annál könnyebben tudunk közel maradni a középpontjához, és ezért ösztönösen mindannyian egy hosszú lépést teszünk meg instabil felületen állva. Vagyis a támasztó terület nemcsak maguk a lábak, hanem a köztük lévő tér is.

Azt is fontos tudni, hogy a támasztófelület területének szélessége jobban befolyásolja, mint a hossza. Ez egy ember esetében azt jelenti, hogy nagyobb eséllyel esünk az oldalunkra, mint hátra, és még inkább előre. Ezért futás közben nehezebben tartjuk meg az egyensúlyt, ugyanez mondható el a sarkúról is. De a széles, stabil cipőben éppen ellenkezőleg, könnyebb ellenállni, még könnyebb, mint teljesen mezítláb. Az elején említett tevékenységekhez azonban nagyon puha, könnyű lábbelire van szükség, vagy egyáltalán nem. Ezért cipővel nem tudunk segíteni magunkon.

Ezért nagyon fontos, hogy megtalálja a lábán lévő függőleges vonal középpontját. Általában nem a láb közepén helyezkedik el, ahogy egyesek automatikusan feltételezik, hanem közelebb a sarokhoz, valahol félúton a láb közepétől a sarok felé.
De ez még nem minden.

A súlypont függőleges vonala mellett van egy vízszintes is, valamint egy külön a végtagoknak.
A nők és férfiak vízszintes vonala kissé eltérően fut.

Előre a nőknél alacsonyabb, a férfiaknál magasabbra megy. Férfiaknál valahol 4-5 ujjal a köldök alatt, nőknél 10 ujjal kb. A női vonal mögött szinte egy koopchik fut, a férfi vonal pedig körülbelül öt ujjal magasabban van nála. Ezenkívül a meditáció közbeni stabilitás érdekében fontos figyelni a térd súlypontjának puszta vonalára. Kissé a csont felett helyezkedik el (alsó lábszár), de két-három ujjal a porc alatt.

Meditáció közben, valamint hastánc közben nem túl jó a lábfejet szélesre tárni, a maximális szélesség általában a vállak szélességének felel meg.

Ezért egy kicsit segítenie kell magát a térdével, próbálva a függőleges tengelyt a lehető legegyenesebbre építeni. Állj a tükör elé, keresd meg magadon az összes leírt pontot. Tegye a lábát vállszélességre. Lazítsa el a lábak és a test izmait. Ezután egyenesítse ki a hátát anélkül, hogy megerőltené a testét, lazítsa meg a lábát egy enyhe térdhajlítással. Képzeljen el három függőleges vonalat, amelyek mindegyike a törzs hátsó részén, előtte és a térd körül egy megfelelő ponton fut. Próbálja úgy elrendezni a pontokat, hogy a törzs elülső tengelye körülbelül félúton legyen a hát és a térd tengelye között. Ebben az esetben a térdeket nem szabad úgy behajlítani, hogy túlmutassák a lábujjakat, csak enyhén hajlítsanak és jól ellazuljanak. Lehetőleg a súlypont felett, azon a támasztó területen belül, amelyet a lábon találtunk. Ugyanakkor a kezek szabadon helyezhetők az istenekre, vagy a tenyereket a csípőre helyezhetik.

Honnan tudhatod, hogy megtaláltad a súlypontodat?

Érezni fog egy enyhe kilengést, ugyanakkor biztosan tudni fogja, hogy nem fog elesni.